题目内容
17.四面体的一条棱长为x,余下的棱长均为1.(1)把四面体的体积V表示为x的函数f(x)并求出定义域;
(2)求体积V的最大值.
分析 (1)取AD中点E,BC中点F,证明BC⊥面AFD,及EF⊥AD,利用V=$\frac{1}{3}$BC?S△AFD,可把四面体的体积V表示为x的函数f(x)并求出定义域;
(2)利用配方法求体积V的最大值.
解答 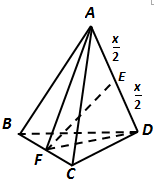 解:如图四面体ABCD中,AD=x,其余各棱为1.取AD中点E,BC中点F
解:如图四面体ABCD中,AD=x,其余各棱为1.取AD中点E,BC中点F
证明BC⊥面AFD,及EF⊥AD
在三角形ABC中,∵三角形ABC为正三角形,F点是BC的中点,
∴AF⊥BC
同理FD⊥BC
∵AF∩FD=F,∴BC⊥面AFD….(3分)
(1)V=$\frac{1}{3}$BC?S△AFD=$\frac{1}{3}$?BC?$\frac{1}{2}$AD?EF=$\frac{1}{6}$BC?AD?EF=$\frac{1}{6}$?1?x?$\sqrt{(\frac{\sqrt{3}}{2})^{2}-(\frac{x}{2})^{2}}$
=$\frac{1}{12}$x$\sqrt{3-{x}^{2}}$
即f(x)=$\frac{1}{12}$x$\sqrt{3-{x}^{2}}$,….(7分)
其中定义域为 x∈(0,$\sqrt{3}$)….(8分)
(2)V=$\frac{1}{12}$$\sqrt{3{x}^{2}-{x}^{4}}$=$\frac{1}{12}$$\sqrt{-({x}^{2}-\frac{3}{2})^{2}+\frac{9}{4}}$,当x=$\frac{\sqrt{6}}{2}$时,Vmax=$\frac{1}{8}$….(12分)
点评 本题考查体积的计算,考查配方法,考查学生分析解决问题的能力,正确求体积是关键.

练习册系列答案
相关题目
5.如图是一个正方体的平面展开图,则在正方体中直线AB与CD的位置关系为( )


| A. | 相交 | B. | 平行 | C. | 异面而且垂直 | D. | 异面但不垂直 |
12.直线a∥b,b⊥c,则a与c的关系是( )
| A. | 异面 | B. | 平行 | C. | 垂直 | D. | 相交 |
2.正方体ABCD-A1B1C1D1中,与棱AB异面的棱有( )
| A. | 2条 | B. | 4条 | C. | 6条 | D. | 8条 |
6.空间中,两条直线若没有交点,则这两条直线的位置关系是( )
| A. | 相交 | B. | 平行 | C. | 异面 | D. | 平行或异面 |
 已知BC为圆O的直径,点A为圆周上一点,AD⊥BC于点D,过点A作圆O的切线交BC的延长线于点P,过点B作BE垂直PA的延长线于点E.求证:
已知BC为圆O的直径,点A为圆周上一点,AD⊥BC于点D,过点A作圆O的切线交BC的延长线于点P,过点B作BE垂直PA的延长线于点E.求证: 如图,在三棱锥P-ABC中,AB=5,BC=4,AC=3,点D是线段PB的中点,平面PAC⊥平面ABC.
如图,在三棱锥P-ABC中,AB=5,BC=4,AC=3,点D是线段PB的中点,平面PAC⊥平面ABC.