题目内容
平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,-2),点C满足 ,其中
,其中 ,且
,且
(1)求点C的轨迹方程;(2)设点C的轨迹与双曲线 交于两点M、N,且以MN为直径的圆过原点,若双曲线的离心率不大于
交于两点M、N,且以MN为直径的圆过原点,若双曲线的离心率不大于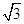 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
 ,其中
,其中 ,且
,且
(1)求点C的轨迹方程;(2)设点C的轨迹与双曲线
 交于两点M、N,且以MN为直径的圆过原点,若双曲线的离心率不大于
交于两点M、N,且以MN为直径的圆过原点,若双曲线的离心率不大于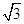 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围. (1)点C的轨迹方程为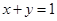 ;(2)双曲线实轴长的取值范围是(0,1].
;(2)双曲线实轴长的取值范围是(0,1].
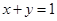 ;(2)双曲线实轴长的取值范围是(0,1].
;(2)双曲线实轴长的取值范围是(0,1].(1)设C(x,y),根据 ,用
,用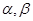 表示x,y,再利用
表示x,y,再利用 ,可得x,y满足的关系式,即点C的轨迹方程.
,可得x,y满足的关系式,即点C的轨迹方程.
(2)点C的轨迹方程与双曲线方程联立消去y后得到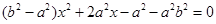 ,
,
然后把题目条件以MN为直径的圆过原点,转化为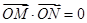 再坐标化得
再坐标化得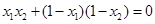 ,即
,即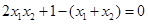 ,借助韦达定理可得到
,借助韦达定理可得到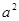 和
和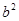 的关系式,从而再借助
的关系式,从而再借助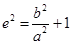 的取范围,确定出a的取值范围,问题得解.
的取范围,确定出a的取值范围,问题得解.
解:设C(x,y),因为 ,则
,则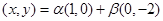
即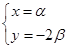
由 ,得
,得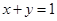 ,即点C的轨迹方程为
,即点C的轨迹方程为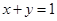 ……4分
……4分
(2)由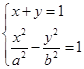 ,得
,得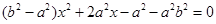
依题意知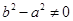 ,设
,设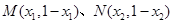
则
因为以MN为直径的圆过原点,所以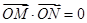
即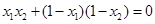 ,即
,即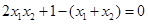
得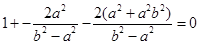 ,得
,得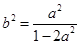 ……………8分
……………8分
∵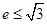 ,∴
,∴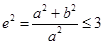 ,∴
,∴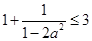
又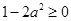 ,∴
,∴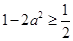 ,∴
,∴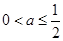 ,从而
,从而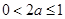
∴双曲线实轴长的取值范围是(0,1].……………12分
 ,用
,用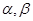 表示x,y,再利用
表示x,y,再利用 ,可得x,y满足的关系式,即点C的轨迹方程.
,可得x,y满足的关系式,即点C的轨迹方程.(2)点C的轨迹方程与双曲线方程联立消去y后得到
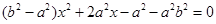 ,
,然后把题目条件以MN为直径的圆过原点,转化为
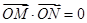 再坐标化得
再坐标化得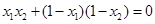 ,即
,即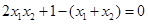 ,借助韦达定理可得到
,借助韦达定理可得到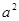 和
和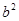 的关系式,从而再借助
的关系式,从而再借助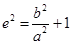 的取范围,确定出a的取值范围,问题得解.
的取范围,确定出a的取值范围,问题得解.解:设C(x,y),因为
 ,则
,则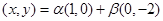
即
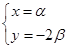
由
 ,得
,得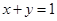 ,即点C的轨迹方程为
,即点C的轨迹方程为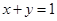 ……4分
……4分(2)由
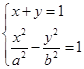 ,得
,得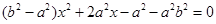
依题意知
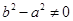 ,设
,设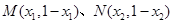
则

因为以MN为直径的圆过原点,所以
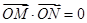
即
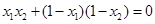 ,即
,即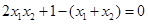
得
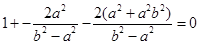 ,得
,得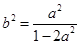 ……………8分
……………8分∵
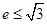 ,∴
,∴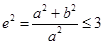 ,∴
,∴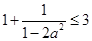
又
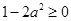 ,∴
,∴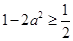 ,∴
,∴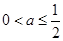 ,从而
,从而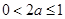
∴双曲线实轴长的取值范围是(0,1].……………12分

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
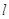 分别交平行四边形
分别交平行四边形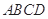 的边
的边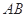 和
和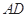 于点
于点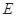 和
和 ,设
,设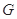 是直线
是直线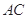 的交点.设
的交点.设
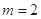 ,
,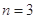 ,试用
,试用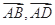 表示
表示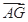 ;
;
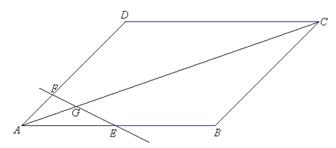
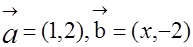 且
且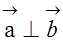 ,则实数x等于 ( )
,则实数x等于 ( )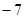
 中,
中, ,
, ,
, ,则
,则 .
.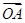 +
+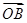 +
+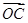 = m
= m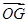 ,则实数m= .
,则实数m= .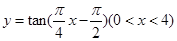 的图象与
的图象与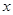 轴交于
轴交于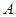 点,过点
点,过点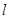 与函数的图象交于
与函数的图象交于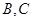 两点, 则
两点, 则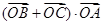
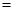 ( )
( )  ,
, ,若
,若 ,则向量
,则向量 与
与 的夹角为( )
的夹角为( )



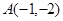 、
、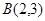 、
、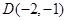 .
. 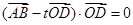 ,求t的值.
,求t的值.