题目内容
正实数a、b、c是等差数列,函数f(x)=ax2+bx+c的图象与x轴有两个交点,则x1•x2的符号是分析:(1)令f(x)=0得到一个一元二次方程,根据韦达定理得到两根之积大于0即可;
(2)函数f(x)的图象与x轴有两个交点,令f(x)=0根的判别式大于0即(
)2-4ac>0①且a,b,c成等差数列即2b=a+c②,将②代入①化简求出x1•x2的范围即可.
(2)函数f(x)的图象与x轴有两个交点,令f(x)=0根的判别式大于0即(
| a+c |
| 2 |
解答:解:(1)令f(x)=0,得到ax2+bx+c=0为一个一元二次方程,
根据韦达定理可知x1•x2=
,因为a>0且c>0得到x1•x2的符号为正;
(2)由题知a、b、c是等差数列,则2b=a+c即b=
,
因为函数图象与x轴有两个交点,得到△=b2-4ac>0,
即(
)2-4ac>0,化简得a2+c2-14ac>0,两边都除以a2得:(
)2-14•
+1>0,
设t=x1•x2=
,则不等式变为:t2-14t+1>0,
化简得:[t-(7+4
)][t-(7-4
)]>0,
所以t>7+4
或t<7-4
则x1•x2的取值范围是(0,7-4
)∪(7+4
,+∞).
故答案为:正,(0,7-4
)∪(7+4
,+∞)
根据韦达定理可知x1•x2=
| c |
| a |
(2)由题知a、b、c是等差数列,则2b=a+c即b=
| a+c |
| 2 |
因为函数图象与x轴有两个交点,得到△=b2-4ac>0,
即(
| a+c |
| 2 |
| c |
| a |
| c |
| a |
设t=x1•x2=
| c |
| a |
化简得:[t-(7+4
| 3 |
| 3 |
所以t>7+4
| 3 |
| 3 |
则x1•x2的取值范围是(0,7-4
| 3 |
| 3 |
故答案为:正,(0,7-4
| 3 |
| 3 |
点评:考查学生灵活运用二次函数图象与性质解决数学问题,灵活运用等差数列的性质及韦达定理化简求值.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
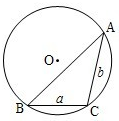 通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长,R表示△ABC外接圆半径.
通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长,R表示△ABC外接圆半径.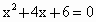 没有实数根.
没有实数根.
 ;
;