题目内容
 如图,椭圆
如图,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆方程;
(2)设F1、F2分别为椭圆的左、右焦点,M为线段AF2的中点,求tan∠ATM.
分析:(1)直线AB方程与椭圆方程联解,利用根的判别式算出a2+4b2-4=0.再由椭圆的离心率e=
,得a=2b,代入前面的式子可得a2=2且b2=
,从而得到椭圆方程;
(2)由(1)算出F1、F2的坐标,从而得到AF2的中点M(1+
,0),联解AB方程与椭圆方程得T(1,
).
最后利用直线的斜率公式和两角差的正切公式,即可得到tan∠ATM的值.
| ||
| 2 |
| 1 |
| 2 |
(2)由(1)算出F1、F2的坐标,从而得到AF2的中点M(1+
| ||
| 4 |
| 1 |
| 2 |
最后利用直线的斜率公式和两角差的正切公式,即可得到tan∠ATM的值.
解答:解:(1)过点A、B的直线方程为:
+y=1,
∵直线AB与椭圆有唯一公共点,
∴将y=1-
x代入椭圆方程,化简得
方程(b2+
a2)x2-a2x+a2-a2b2=0有惟一解,
∴△=a2b2(a2+4b2-4)=0(ab≠0),
故a2+4b2-4=0.
又∵椭圆的离心率e=
,
∴a=2b,代入上式可得a2=2,b2=
,
因此,所求的椭圆方程为
+
=1;
(2)由(1)得c=
=
,得F1(-
,0),F2(-
,0)
从而算出M(1+
,0)
将直线AB方程与椭圆方程联解,可得T(1,
).
∴tan∠AF1T=
=
-1,
又∵tan∠TAM=-
=
,tan∠TMF2=-
=
,
∴tan∠ATM=tan(∠TMF2-∠TAM)=
=
-1.
| x |
| 2 |
∵直线AB与椭圆有唯一公共点,
∴将y=1-
| 1 |
| 2 |
方程(b2+
| 1 |
| 4 |
∴△=a2b2(a2+4b2-4)=0(ab≠0),
故a2+4b2-4=0.
又∵椭圆的离心率e=
| ||
| 2 |
∴a=2b,代入上式可得a2=2,b2=
| 1 |
| 2 |
因此,所求的椭圆方程为
| x2 |
| 2 |
| y2 | ||
|
(2)由(1)得c=
| a2-b2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
从而算出M(1+
| ||
| 4 |
将直线AB方程与椭圆方程联解,可得T(1,
| 1 |
| 2 |
∴tan∠AF1T=
| ||||
1+
|
| ||
| 2 |
又∵tan∠TAM=-
| ||
| 1-2 |
| 1 |
| 2 |
| ||||
1-(1+
|
| 2 | ||
|
∴tan∠ATM=tan(∠TMF2-∠TAM)=
| ||||||
1+
|
| ||
| 2 |
点评:本题给出椭圆满足的条件,求椭圆的方程并求角的正切之值.主要考查了直线与椭圆的位置关系、椭圆的几何性质,同时考查解析几何的基本思想方法和综合解题能力,属于中档题.

练习册系列答案
相关题目
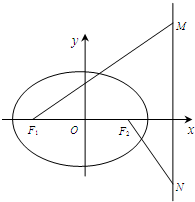 如图,椭圆
如图,椭圆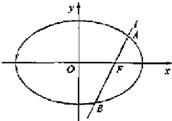 如图,椭圆
如图,椭圆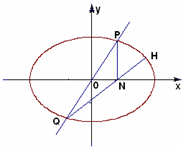 如图,椭圆
如图,椭圆 (2010•武清区一模)如图,椭圆
(2010•武清区一模)如图,椭圆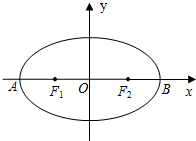 如图,椭圆
如图,椭圆