题目内容
给出下列命题:
①已知a,b,m都是正数,且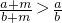 ,则a<b;
,则a<b;
②当x∈(1,+∞)时,函数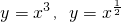 的图象都在直线y=x的上方;;
的图象都在直线y=x的上方;;
③命题“?x∈R,使得x2-2x+1<0”的否定是真命题;
④“|x|≤1,且|y|≤1”是“|x+y|≤2”的充分不必要条件.
其中正确命题的序号是________.(把你认为正确命题的序号都填上)
①③④
分析:利用不等式的性质判断出①对;利用幂函数的图象判断出②错;利用命题的否定与原命题真假相反判断出③对;利用绝对值的性质及充要条件的定义判断出④对.
解答:对于:①已知a,b,m都是正数,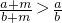 ?ab+bm>ab+am?a<b;正确;
?ab+bm>ab+am?a<b;正确;
对于②,因为当x∈(1,+∞)时,函数y=x3的图象都在直线y=x的上方;但函数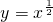 的图象都在直线y=x的下方;所以②错误;
的图象都在直线y=x的下方;所以②错误;
对于③,因为x2-2x+1=(x-1)2≥0恒成立,所以命题“?x∈R,使得x2-2x+1<0”为假命题,所以命题“?x∈R,使得x2-2x+1<0”的否定是真命题;所以③正确;
对于④,因为||x|-|y||≤|x+y|≤|x|+|y|,所以若④“|x|≤1,且|y|≤1”成立,则|≤|x|+|y|≤2,所以“|x+y|≤2”成立,反之“|x+y|≤2”例如x=-1,y=3满足,但不满足④“|x|≤1,且|y|≤1”,所以“|x|≤1,且|y|≤1”是“|x+y|≤2”的充分不必要条件,所以④正确.
故答案为:①③④.
点评:本题考查绝对值的性质:||x|-|y||≤|x+y|≤|x|+|y|,考查充要条件的判断方法,是一道综合题.
分析:利用不等式的性质判断出①对;利用幂函数的图象判断出②错;利用命题的否定与原命题真假相反判断出③对;利用绝对值的性质及充要条件的定义判断出④对.
解答:对于:①已知a,b,m都是正数,
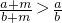 ?ab+bm>ab+am?a<b;正确;
?ab+bm>ab+am?a<b;正确;对于②,因为当x∈(1,+∞)时,函数y=x3的图象都在直线y=x的上方;但函数
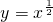 的图象都在直线y=x的下方;所以②错误;
的图象都在直线y=x的下方;所以②错误;对于③,因为x2-2x+1=(x-1)2≥0恒成立,所以命题“?x∈R,使得x2-2x+1<0”为假命题,所以命题“?x∈R,使得x2-2x+1<0”的否定是真命题;所以③正确;
对于④,因为||x|-|y||≤|x+y|≤|x|+|y|,所以若④“|x|≤1,且|y|≤1”成立,则|≤|x|+|y|≤2,所以“|x+y|≤2”成立,反之“|x+y|≤2”例如x=-1,y=3满足,但不满足④“|x|≤1,且|y|≤1”,所以“|x|≤1,且|y|≤1”是“|x+y|≤2”的充分不必要条件,所以④正确.
故答案为:①③④.
点评:本题考查绝对值的性质:||x|-|y||≤|x+y|≤|x|+|y|,考查充要条件的判断方法,是一道综合题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.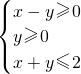 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.