Question

【题目】若函数f（x）=kax﹣a﹣x（a＞0且a≠1）在（﹣∞，+∞）上既是奇函数又是增函数，则函数g（x）=loga（x+k）的图象是（ ）
A.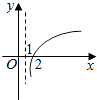
B.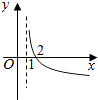
C.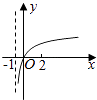
D.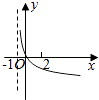

Answer 1

【答案】C
【解析】解：∵函数f（x）=kax﹣a﹣x，（a＞0，a≠1）在（﹣∞，+∞）上是奇函数

则f（﹣x）+f（x）=0

即（k﹣1）（ax﹣a﹣x）=0

则k=1

又∵函数f（x）=kax﹣a﹣x，（a＞0，a≠1）在（﹣∞，+∞）上是增函数

则a＞1

则g（x）=loga（x+k）=loga（x+1）

函数图象必过原点，且为增函数

故选C

由函数f（x）=kax﹣a﹣x，（a＞0，a≠1）在（﹣∞，+∞）上既是奇函数，又是增函数，则由复合函数的性质，我们可得k=1，a＞1，由此不难判断函数的图象．