题目内容
已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据,
(Ⅰ)求这个组合体的体积;
(Ⅱ)若组合体的底部几何体记为ABCD-A1B1C1D1,其中A1B1BA为正方形.
(i)求证:A1B⊥平面AB1C1D;
(ii)求证:P为棱A1B1上一点,求AP+PC1的最小值.
分析:(I)由几何体的三视图可知该几何体为底部为长方体,(该长方体的棱长分别为8,8,10),上部为半个圆柱(圆柱的底面直径为8,高为10)代入体积公式可求
(II)(i)由长方体的性质易得A1B⊥AD,A1B⊥AB1,根据直线与平面垂直的判定定理可证
(ii)将上底面A1B1C1D1展开,与平面A1B1BA共面时,连接AC1交A1B1于点P,即AC1为最短距离
(II)(i)由长方体的性质易得A1B⊥AD,A1B⊥AB1,根据直线与平面垂直的判定定理可证
(ii)将上底面A1B1C1D1展开,与平面A1B1BA共面时,连接AC1交A1B1于点P,即AC1为最短距离
解答:解:(Ⅰ)此组合体底部为长方体,上部为半个圆柱V=8×8×10+
π×42×10=640+80π.(5分)
(Ⅱ)(i)∵长方体ABCD-A1B1C1D1
∴AD⊥平面A1B1BA
∵A1B?平面A1B1BA
∴AD⊥A1B
又∵A1B1BA是边长为8的正方形
∴A1B⊥AB1
∵AB1∩AD=A
∴A1B⊥平面AB1C1D.(10分)
(ii)将上底面A1B1C1D1展开,与平面A1B1BA共面时,连接C1A交A1B1于点P,即AC1为最短距离.
此时长度为
=2
.(13分)
| 1 |
| 2 |
(Ⅱ)(i)∵长方体ABCD-A1B1C1D1
∴AD⊥平面A1B1BA
∵A1B?平面A1B1BA
∴AD⊥A1B
又∵A1B1BA是边长为8的正方形
∴A1B⊥AB1
∵AB1∩AD=A
∴A1B⊥平面AB1C1D.(10分)
(ii)将上底面A1B1C1D1展开,与平面A1B1BA共面时,连接C1A交A1B1于点P,即AC1为最短距离.
此时长度为
| 82+182 |
| 97 |
点评:本题主要考查了由三视图还原实物图的能力,直线与平面垂直的判定定理的应用,平面展开图的运用你,解决此题的关键是要求考生具备很强的空间想象能力.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
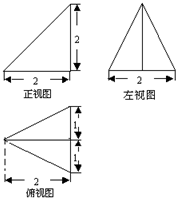 已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( ) (1)已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中的数据,求这个组合体的体积;
(1)已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中的数据,求这个组合体的体积; 已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的表面积是( )
已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的表面积是( )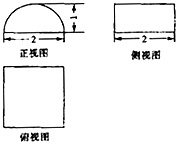 已知某个几何体的三视图如图(正视图中的弧线是半圆),图中标出的尺(单位:cm),可得这个几何体表面是
已知某个几何体的三视图如图(正视图中的弧线是半圆),图中标出的尺(单位:cm),可得这个几何体表面是