题目内容
如果定义域为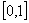 的函数
的函数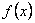 同时满足以下三个条件:
同时满足以下三个条件:
① 对任意的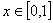 ,总有
,总有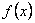 ≥0;
≥0;
②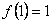
 ;
;
③若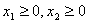 且
且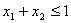 ,则有
,则有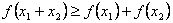 成立。
成立。
那么称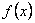 为“友谊函数”。
为“友谊函数”。
请解答下列各题:
(1)若已知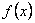 为“友谊函数”,求
为“友谊函数”,求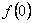 的值;
的值;
(2)函数 在区间
在区间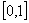 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知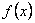 为“友谊函数”,假定存在
为“友谊函数”,假定存在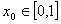 ,使得
,使得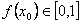 且
且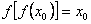 ,求证:
,求证: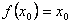
【答案】
解:(1)取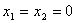 得
得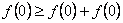 ,又由
,又由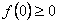 ,得
,得
(2)显然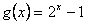 在
在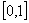 上满足①
上满足①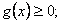 ②
②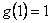 ,
,
若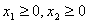 ,且
,且 ,则有
,则有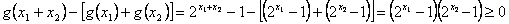
故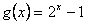 满足条件①﹑②﹑③所以
满足条件①﹑②﹑③所以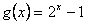 为友谊函数.
为友谊函数.
(3)由③知任给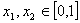 其中
其中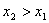 ,且有
,且有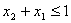 ,则0<
,则0< <1,
<1,
所以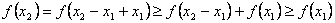
依题意必有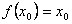 ,下面用反证法证明:
,下面用反证法证明:
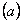 若
若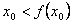 ,则
,则 ,这与
,这与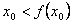 矛盾;
矛盾;
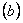 若
若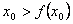 ,则
,则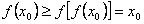 ,这与
,这与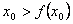 矛盾
矛盾
故由上述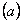 ﹑
﹑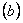 证明知假设不成立,则必有
证明知假设不成立,则必有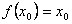 成立.
成立.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
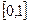 的函数
的函数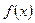 同时满足以下三个条件:
同时满足以下三个条件: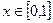 ,总有
,总有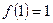 ;
;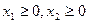 且
且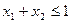 ,则有
,则有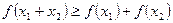 成立,并且称
成立,并且称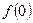 的值;
的值;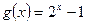 在区间
在区间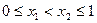 ,求证:
,求证: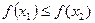
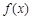 的定义域为
的定义域为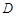 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的“高调函数”.现给出下列命题:
上的“高调函数”.现给出下列命题: 为
为 上的“1高调函数”;
上的“1高调函数”; 为
为 高调函数”;
高调函数”; 的函数
的函数 为
为 高调函数”,那么实数
高调函数”,那么实数 ;
; 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数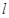 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的
上的 的函数
的函数 时,
时, ,且
,且 的取值范围是
的取值范围是
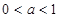 . B.
. B. 
 D.
D.
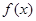 的定义域为
的定义域为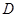 ,若存在非零实数
,若存在非零实数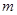 满足对于任意
满足对于任意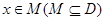 ,均有
,均有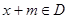 ,且
,且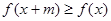 ,则称
,则称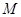 上的
上的 的函数
的函数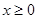 时,
时,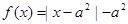 ,且
,且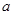 的取值范围是( )
的取值范围是( ) 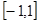 B.
B.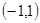 C.
C.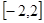 D.
D.