题目内容
设函数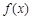 的定义域为
的定义域为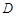 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称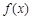 为
为 上的“高调函数”.现给出下列命题:
上的“高调函数”.现给出下列命题:
①函数 为
为 上的“1高调函数”;
上的“1高调函数”;
②函数 为
为 上的“
上的“ 高调函数”;
高调函数”;
③如果定义域为 的函数
的函数 为
为 上“
上“ 高调函数”,那么实数
高调函数”,那么实数 的取值范围是
的取值范围是 ;
;
其中正确的命题是 .(写出所有正确命题的序号)
【答案】
①②③
【解析】∵函数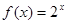 为R上的递增函数,所以
为R上的递增函数,所以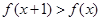 ,故①正确,
,故①正确,
∵sin2(x+π)≥sin2x,∴函数f(x)=sin2x为R上的π高调函数,故②正确,
∵如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上m高调函数,
只有[-1,1]上至少需要加2,那么实数m的取值范围是[2,+∞),故③正确,
故答案为:①②③

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 的定义域为
的定义域为 ,若满足:①
,若满足:①
 ,使得
,使得 上的值域为
上的值域为 是定义域为
是定义域为 是定义域为
是定义域为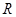 的“成功函数”,则
的“成功函数”,则 的取值范围为 ( )
的取值范围为 ( )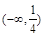 B.
B.
 C.
C.
 D.
D.

 的定义域为
的定义域为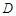 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的“
上的“ 高调函数”.现给出下列命题:
高调函数”.现给出下列命题: 为
为 上的“1高调函数”;
上的“1高调函数”; 为
为 高调函数”;
高调函数”; 的函数
的函数 为
为 高调函数”,那么实数
高调函数”,那么实数 ;
;