题目内容
设两个向量 ,
, 满足|
满足|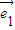 |=2,|
|=2,| |=1,
|=1,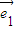 与
与 的夹角为
的夹角为 ,若向量2t
,若向量2t +7
+7 与
与 +t
+t 的夹角为钝角,则实数t的范围为 .
的夹角为钝角,则实数t的范围为 .
【答案】分析:根据向量2t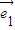 +7
+7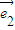 与
与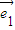 +t
+t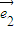 的夹角为钝角,得其数量积小于0,展开后得到关于t的不等式求解t的范围,然后除掉两向量共线反向时的t的值.
的夹角为钝角,得其数量积小于0,展开后得到关于t的不等式求解t的范围,然后除掉两向量共线反向时的t的值.
解答:解:由向量2t +7
+7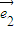 与
与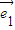 +t
+t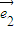 的夹角为钝角,得
的夹角为钝角,得 ,
,
即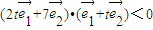 ,
,
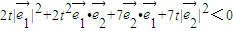 ,
,
化简即得2t2+15t+7<0,
解得-7<t<- ,
,
当夹角为π时,也有 ,
,
但此时夹角不是钝角,
设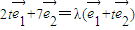 ,λ<0,
,λ<0,
则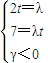 ,∴
,∴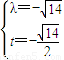
∴所求实数t的范围是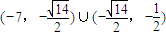 .
.
点评:本题考查了平面向量数量积的运算,两向量夹角为锐角,数量积大于0,夹角为钝角,数量积小于0,注意数量积小于0时夹角还有180°的情况,此题是中档题,也是易错题.
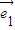 +7
+7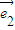 与
与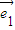 +t
+t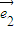 的夹角为钝角,得其数量积小于0,展开后得到关于t的不等式求解t的范围,然后除掉两向量共线反向时的t的值.
的夹角为钝角,得其数量积小于0,展开后得到关于t的不等式求解t的范围,然后除掉两向量共线反向时的t的值.解答:解:由向量2t
 +7
+7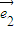 与
与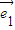 +t
+t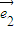 的夹角为钝角,得
的夹角为钝角,得 ,
,即
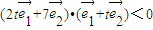 ,
,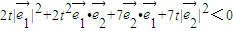 ,
,化简即得2t2+15t+7<0,
解得-7<t<-
 ,
,当夹角为π时,也有
 ,
,但此时夹角不是钝角,
设
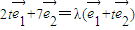 ,λ<0,
,λ<0,则
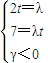 ,∴
,∴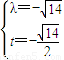
∴所求实数t的范围是
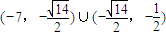 .
.点评:本题考查了平面向量数量积的运算,两向量夹角为锐角,数量积大于0,夹角为钝角,数量积小于0,注意数量积小于0时夹角还有180°的情况,此题是中档题,也是易错题.

练习册系列答案
相关题目
 ,
, 满足|
满足| |=2,|
|=2,| |=1,
|=1, ,
, 的夹角为60°,
的夹角为60°, =2x
=2x +7
+7 ,
, =
= +x
+x ,x∈R.
,x∈R. ,
, 的夹角为钝角,求x的取值范围;
的夹角为钝角,求x的取值范围; •
• ,求f(x)在[-1,1]上的最大值与最小值.
,求f(x)在[-1,1]上的最大值与最小值.