题目内容
已知两个向量 ,
, 满足|
满足| |=2,|
|=2,| |=1,
|=1, ,
, 的夹角为60°,
的夹角为60°, =2x
=2x +7
+7 ,
, =
= +x
+x ,x∈R.
,x∈R.(1)若
 ,
, 的夹角为钝角,求x的取值范围;
的夹角为钝角,求x的取值范围;(2)设函数f(x)=
 •
• ,求f(x)在[-1,1]上的最大值与最小值.
,求f(x)在[-1,1]上的最大值与最小值.
【答案】分析:(1)先确定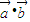 的值,再由
的值,再由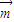 ,
,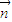 的夹角为钝角可知
的夹角为钝角可知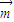 •
•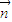 <0,代入即可解题.
<0,代入即可解题.
(2)根据(1)中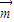 •
•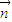 的值确定函数f(x)的解析式,再根据二次函数的单调性求出在[-1,1]上的最大值与最小值.
的值确定函数f(x)的解析式,再根据二次函数的单调性求出在[-1,1]上的最大值与最小值.
解答:解:(1)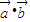 =|a||b|cos60°=2×1×cos60°=1,
=|a||b|cos60°=2×1×cos60°=1,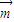 ,
,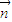 的夹角为钝角,得
的夹角为钝角,得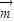 •
•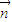 <0,且
<0,且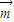 ≠λ
≠λ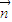
∴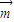 •
•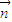 =(2x
=(2x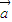 +7
+7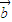 )•(
)•(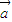 +x
+x )=2x
)=2x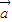 2+2
2+2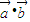 +2x2
+2x2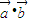 +7
+7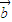 2
2
=8x+2x2+7+7x
=2x2+15x+7<0
解得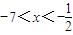 ,
,
 ≠λ
≠λ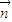
可得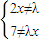 ,解得x≠
,解得x≠
∴x的取值范围是 ;
;
(2)由(1)得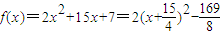 ,f(x)在[-1,1]上单调递增,
,f(x)在[-1,1]上单调递增,
∴f(x)min=f(-1)=2-15+7=-1,f(x)max=f(1)=2+15+7=24.
点评:本题主要考查向量的点乘运算和二次函数的最值问题.属基础题.
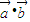 的值,再由
的值,再由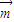 ,
,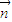 的夹角为钝角可知
的夹角为钝角可知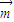 •
•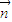 <0,代入即可解题.
<0,代入即可解题.(2)根据(1)中
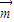 •
•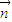 的值确定函数f(x)的解析式,再根据二次函数的单调性求出在[-1,1]上的最大值与最小值.
的值确定函数f(x)的解析式,再根据二次函数的单调性求出在[-1,1]上的最大值与最小值.解答:解:(1)
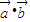 =|a||b|cos60°=2×1×cos60°=1,
=|a||b|cos60°=2×1×cos60°=1,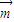 ,
,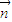 的夹角为钝角,得
的夹角为钝角,得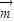 •
•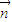 <0,且
<0,且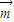 ≠λ
≠λ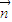
∴
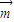 •
•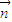 =(2x
=(2x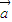 +7
+7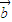 )•(
)•(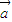 +x
+x )=2x
)=2x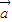 2+2
2+2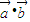 +2x2
+2x2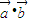 +7
+7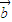 2
2=8x+2x2+7+7x
=2x2+15x+7<0
解得
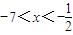 ,
, ≠λ
≠λ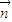
可得
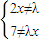 ,解得x≠
,解得x≠
∴x的取值范围是
 ;
;(2)由(1)得
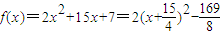 ,f(x)在[-1,1]上单调递增,
,f(x)在[-1,1]上单调递增,∴f(x)min=f(-1)=2-15+7=-1,f(x)max=f(1)=2+15+7=24.
点评:本题主要考查向量的点乘运算和二次函数的最值问题.属基础题.

练习册系列答案
相关题目
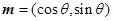 ,
, ,其中
,其中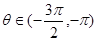 ,且满足
,且满足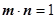 .
.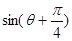 的值; (Ⅱ)求
的值; (Ⅱ)求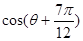 的值.
的值.