题目内容
【题目】已知矩阵A的逆矩阵A﹣1=( ![]() ).
).
(1)求矩阵A;
(2)求矩阵A﹣1的特征值以及属于每个特征值的一个特征向量.
【答案】
(1)解:设A= ![]() ,则由AA﹣1=E得
,则由AA﹣1=E得 ![]()
![]() =
= ![]() ,
,
解得a= ![]() ,b=﹣
,b=﹣ ![]() ,c=﹣
,c=﹣ ![]() ,d=
,d= ![]() ,所以A=
,所以A= 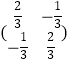
(2)解:矩阵A﹣1的特征多项式为f(λ)= ![]() =(λ﹣2)2﹣1,
=(λ﹣2)2﹣1,
令f(λ)=(λ﹣2)2﹣1=0,可求得特征值为λ1=1,λ2=3,
设λ1=1对应的一个特征向量为α= ![]() ,
,
则由λ1α=Mα,得x+y=0
得x=﹣y,可令x=1,则y=﹣1,
所以矩阵M的一个特征值λ1=1对应的一个特征向量为 ![]() ,
,
同理可得矩阵M的一个特征值λ2=3对应的一个特征向量为 ![]()
【解析】(1)利用AA﹣1=E,建立方程组,即可求矩阵A;(2)先根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量.

 学习实践园地系列答案
学习实践园地系列答案【题目】某中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
男 | 女 | |
文科 | 2 | 5 |
理科 | 10 | 3 |
(1)若在该样本中从报考文科的女学生A.B.C.D.E中随机地选出2人召开座谈会,试求2人中有A的概率;
(2)用假设检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关?
参考公式和数据:![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 总计 | |
男性市民 |
| ||
女性市民 |
| ||
总计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过![]() 的前提下认为支持申办
的前提下认为支持申办![]() 年足球世界杯与性别有关?请说明理由.
年足球世界杯与性别有关?请说明理由.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|