Question

已知不等式组

4x-3y+m≤0 x＞0 y＜0

，
（1）若该不等式组表示的平面区域内的整点有且仅有一个，且在直线4x-3y+m=0上，则实数m=

-7

；
（2）若该不等式组表示的平面区域内的整点有且仅有三个，则实数m的取值范围是

（-13，-11]

．

Answer 1

分析：（1）作出不等式组表示的平面区域，得到如图的△AB0内部，不等式组表示的平面区域内的整点有且仅有一个，必定是（-1，1），因此（-1，1）在直线4x-3y+m=0上，可解出m=7；
（2）记直线l：4x-3y+m=0，随着l向上平移，可见区域内依此出现点（-1，1）、（-1，2）、（-2，1）、（-1，3），由此建立关于m的不等式组，解之即可得到实数m的范围．

解答：解：作出不等式组

4x-3y+m≤0 x＞0 y＜0

表示的平面区域，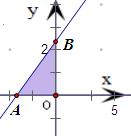
得到如图的△AB0内部，其中A（-

m

4

，0），B（0，

m

3

），0为坐标原点
（1）∵不等式组表示的平面区域内的整点有且仅有一个，
∴必定有（-1，1）在区域内，故点（-1，1）在直线4x-3y+m=0上，
即4×（-1）-3×1+m=0，解之得m=7；
（2）结合直线的斜率k=

4

3

，平移直线l：4x-3y+m=0
随着直线l的向上平移，区域内依此出现点
（-1，1）、（-1，2）、（-2，1）、（-1，3）
∴若该不等式组表示的平面区域内的整点有且仅有三个，必定是（-1，1）、（-1，2）、（-2，1）
记F（x，y）=4x-3y+m=0，则

F(-2，1)≤0 F(-1，3)＞0

即

-8-3+m≤0 -4-9+m＞0

，解之得-13＜m≤-11
故答案为：7，-13＜m≤-11

点评：本题给出含有字母参数的不等式组，在已知区域内整点个数的情况下求参数的值或范围．着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于中档题．