题目内容
已知点M在曲线x2+y2+4x+3=0上,点N在不等式组
所表示的平面区域内,那么|MN|的最小值是( )
|
分析:曲线x2+y2+4x+3=0化为标准方程为(x+2)2+y2=1,表示以C(-2,0)为圆心,1为半径的圆;不等式组
所表示的平面区域为一直角三角形,求出C到直线3x+4y=4的距离,即可得到结论.
|
解答:解:曲线x2+y2+4x+3=0化为标准方程为(x+2)2+y2=1,表示以C(-2,0)为圆心,1为半径的圆;不等式组
所表示的平面区域为一直角三角形,
由图形可知,C到直线3x+4y=4的距离为
=2
∴|MN|的最小值是2-1=1
故选A.
|
由图形可知,C到直线3x+4y=4的距离为
| |-6-4| |
| 5 |

∴|MN|的最小值是2-1=1
故选A.
点评:本题考查线性规划知识,考查学生的分析能力,正确画出图形是关键.

练习册系列答案
相关题目
已知点M在曲线x2+y2+4x+3=0,点N在不等式组
所表示的平面区域上,那么|MN|的最小值是( )
|
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
 所表示的平面区域上,那么|MN|的最小值是( )
所表示的平面区域上,那么|MN|的最小值是( )
 -1
-1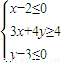 所表示的平面区域上,那么|MN|的最小值是( )
所表示的平面区域上,那么|MN|的最小值是( )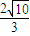
 -1
-1 所表示的平面区域上,那么|MN|的最小值是( )
所表示的平面区域上,那么|MN|的最小值是( )
 -1
-1