题目内容
求值:
(1)已知cos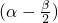 =-
=- ,sin(β-
,sin(β- )=
)= ,且
,且 <α<π,0<β<
<α<π,0<β< ,求cos
,求cos 的值;
的值;
(2)已知tanα=4 ,cos(α+β)=-
,cos(α+β)=- ,α、β均为锐角,求cosβ的值.
,α、β均为锐角,求cosβ的值.
解:(1)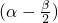 +
+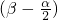 =
= ,
,
∵ <α<π,0<β<
<α<π,0<β< .
.
∴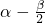 ∈
∈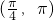 ,
,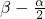 ∈
∈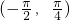
∴sin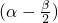 =
=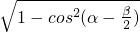 =
= ,cos
,cos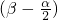 =
= ,
,
∴cos =cos
=cos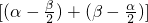 =cos
=cos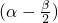 cos
cos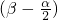 -sin
-sin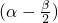 sin
sin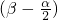
=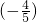 ×
× -
- ×
× =-
=- .
.
(2)∵tanα=4 ,且α为锐角,
,且α为锐角,
∴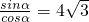 ,即sinα=4
,即sinα=4 cosα,
cosα,
又∵sin2α+cos2α=1,
∴sinα=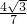 ,cosα=
,cosα= .
.
∵0<α,β< ,
,
∴0<α+β<π,
∴sin(α+β)=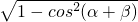 =
=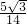 .
.
而β=(α+β)-α,
∴cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα=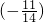 ×
× +
+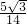 ×
×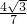 =
= .
.
分析:(1)利用角的变换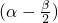 +
+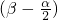 =
= ,确定
,确定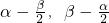 的范围,求出相关三角函数值,即可求出cos
的范围,求出相关三角函数值,即可求出cos 的值;
的值;
(2)根据α为锐角,tanα=4 求出sinα,cosα,借助cosβ=cos[(α+β)-α]展开,求出cosβ的值.
求出sinα,cosα,借助cosβ=cos[(α+β)-α]展开,求出cosβ的值.
点评:本题是基础题,考查三角函数的角的变换的技巧,根据三角函数角的范围求出有关的三角函数的值,是本题解答的关键,考查计算能力.
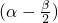 +
+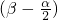 =
= ,
,∵
 <α<π,0<β<
<α<π,0<β< .
.∴
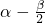 ∈
∈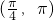 ,
,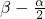 ∈
∈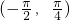
∴sin
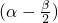 =
=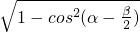 =
= ,cos
,cos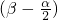 =
= ,
,∴cos
 =cos
=cos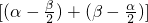 =cos
=cos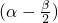 cos
cos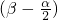 -sin
-sin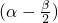 sin
sin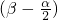
=
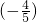 ×
× -
- ×
× =-
=- .
.(2)∵tanα=4
 ,且α为锐角,
,且α为锐角,∴
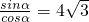 ,即sinα=4
,即sinα=4 cosα,
cosα,又∵sin2α+cos2α=1,
∴sinα=
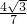 ,cosα=
,cosα= .
.∵0<α,β<
 ,
,∴0<α+β<π,
∴sin(α+β)=
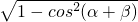 =
=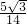 .
.而β=(α+β)-α,
∴cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα=
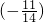 ×
× +
+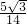 ×
×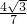 =
= .
.分析:(1)利用角的变换
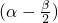 +
+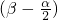 =
= ,确定
,确定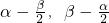 的范围,求出相关三角函数值,即可求出cos
的范围,求出相关三角函数值,即可求出cos 的值;
的值;(2)根据α为锐角,tanα=4
 求出sinα,cosα,借助cosβ=cos[(α+β)-α]展开,求出cosβ的值.
求出sinα,cosα,借助cosβ=cos[(α+β)-α]展开,求出cosβ的值.点评:本题是基础题,考查三角函数的角的变换的技巧,根据三角函数角的范围求出有关的三角函数的值,是本题解答的关键,考查计算能力.

练习册系列答案
相关题目
 【选修4-1:几何证明选讲】
【选修4-1:几何证明选讲】 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤. 如图,已知O为△ABC的外心,a,b,c分别是角A、B、C的对边,且满足
如图,已知O为△ABC的外心,a,b,c分别是角A、B、C的对边,且满足