题目内容
已知圆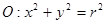 ,点
,点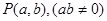 是圆
是圆 内的一点,过点
内的一点,过点 的圆
的圆 的最短弦在直线
的最短弦在直线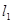 上,直线
上,直线 的方程为
的方程为 ,那么( )
,那么( )
A.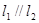 且 且 与圆 与圆 相交 相交 | B. 且 且 与圆 与圆 相切 相切 |
C.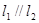 且 且 与圆 与圆 相离 相离 | D. 且 且 与圆 与圆 相离 相离 |
D
解析试题分析:因为点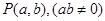 是已知圆内一点,所以
是已知圆内一点,所以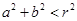 ,过点
,过点 的圆
的圆 的最短弦所在的直线
的最短弦所在的直线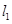 与直线
与直线 垂直,所以
垂直,所以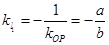 ,而
,而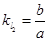 ,所以
,所以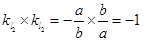 ,所以
,所以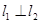 ,圆心
,圆心 到直线
到直线 的距离为
的距离为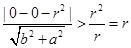 ,从而直线
,从而直线 与圆
与圆 相离,所以选D.
相离,所以选D.
考点:1.直线与圆的位置关系;2.两直线的位置关系.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
直线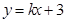 与圆
与圆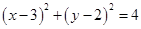 相交于M,N两点,若
相交于M,N两点,若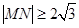 ,则k取值范围是 ( )
,则k取值范围是 ( )
A.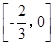 | B.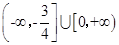 | C.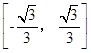 | D.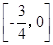 |
若直线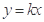 与圆
与圆 的两个交点关于直线
的两个交点关于直线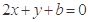 对称,则
对称,则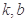 的值分别为( )
的值分别为( )
A.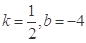 | B.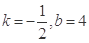 |
C.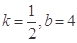 | D.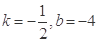 |
圆 与圆
与圆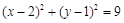 的位置关系为( )
的位置关系为( )
| A.内切 | B.相交 | C.外切 | D.相离 |
过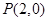 的直线
的直线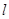 被圆
被圆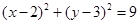 截得的线段长为2时,直线
截得的线段长为2时,直线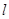 的斜率为( )
的斜率为( )
A.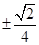 | B.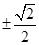 | C.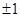 | D.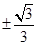 |
已知圆的方程为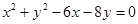 .设该圆过点
.设该圆过点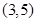 的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A.10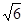 | B.20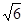 | C.30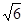 | D.40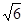 |
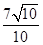 的点的个数为( )
的点的个数为( ) -4
-4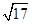 -1
-1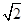 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).