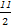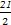题目内容
过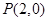 的直线
的直线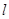 被圆
被圆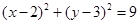 截得的线段长为2时,直线
截得的线段长为2时,直线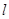 的斜率为( )
的斜率为( )
A.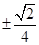 | B.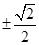 | C.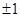 | D.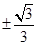 |
A
解析试题分析:由题意直线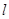 的斜率存在设为
的斜率存在设为 ,则直线
,则直线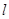 的方程为
的方程为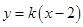 ,即
,即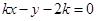 由点到直线的距离公式得,圆心到直线
由点到直线的距离公式得,圆心到直线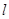 的距离为
的距离为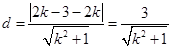 ,由圆的性质可得
,由圆的性质可得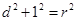 ,即
,即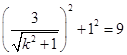 ,解得
,解得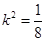 ,即
,即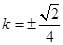 .
.
考点:直线与圆的位置关系.

练习册系列答案
相关题目
已知函数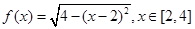 对于满足
对于满足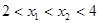 的任意
的任意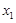 ,
,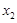 ,给出下列结论:
,给出下列结论:
①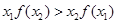
②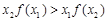
③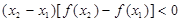
④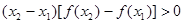
其中正确的是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
已知圆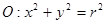 ,点
,点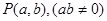 是圆
是圆 内的一点,过点
内的一点,过点 的圆
的圆 的最短弦在直线
的最短弦在直线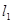 上,直线
上,直线 的方程为
的方程为 ,那么( )
,那么( )
A.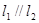 且 且 与圆 与圆 相交 相交 | B. 且 且 与圆 与圆 相切 相切 |
C.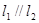 且 且 与圆 与圆 相离 相离 | D. 且 且 与圆 与圆 相离 相离 |
若圆x2+y2-2kx+2y+2=0(k>0)与两坐标轴无公共点,那么实数k的取值范围为( )
| A.-1<k<1 | B.1<k<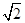 |
| C.1<k<2 | D.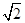 <k<2 <k<2 |
已知点A(1,2),B(3,2),以线段AB为直径作圆C,则直线l:x+y-3=0与圆C的位置关系是( )
| A.相交且过圆心 | B.相交但不过圆心 | C.相切 | D.相离 |
若原点在圆(x-m)2+(y+m)2=8的内部,则实数m的取值范围是( )
A.-2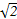 <m<2 <m<2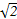 | B.0<m<2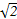 |
| C.-2<m<2 | D.0<m<2 |
垂直于直线y=x+1且与圆x2+y2=1相切于第一象限的直线方程( ).
A.x+y- =0 =0 | B.x+y+1=0 |
| C.x+y-1=0 | D.x+y+ =0 =0 |
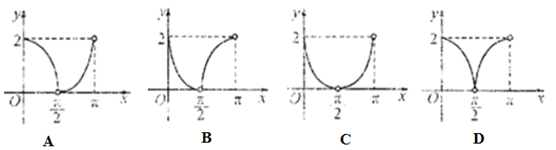
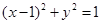 上异于坐标原点O的任意一点,直线OP的倾斜角为 ,若
上异于坐标原点O的任意一点,直线OP的倾斜角为 ,若 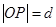 ,则函数
,则函数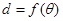 的大致图像是 ( )
的大致图像是 ( )