题目内容
10.在正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BB1的中点,则EF与BC1所成的角为60°.分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出EF与BC1所成的角.
解答 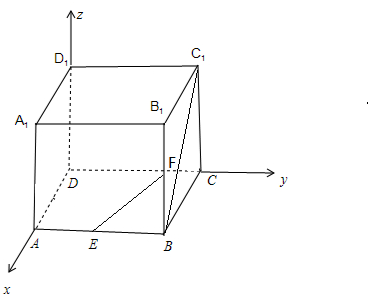 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系
设正方体ABCD-A1B1C1D1的棱长为2,
∵E、F分别是棱AB和BB1的中点,
∴E(2,1,0),F(2,2,1),B(2,2,0),C1(0,2,2),
∴$\overrightarrow{EF}$=(0,1,1),$\overrightarrow{B{C}_{1}}$=(-2,0,2),
∴cos<$\overrightarrow{EF},\overrightarrow{B{C}_{1}}$>=$\frac{2}{\sqrt{2}×\sqrt{8}}$=$\frac{1}{2}$,
∴EF与BC1所成的角为60°.
故答案为:60°.
点评 本题考查异面直线所成角的求法,是基础题,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
15.设A(-2,3),B(3,3),若直线ax+y+2=0与线段AB有交点,则实数a的取值范围是( )
| A. | [-$\frac{5}{3}$,$\frac{5}{2}$] | B. | (-∞,-$\frac{5}{3}$]∪[$\frac{5}{2}$,+∞) | C. | (-∞,-$\frac{5}{2}$]∪[$\frac{5}{3}$,+∞) | D. | [-$\frac{5}{2}$,$\frac{5}{3}$] |
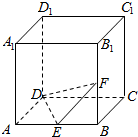 如图,正方体ABCD-A1B1C1D1中,E,F分别为AB与BB1的中点.
如图,正方体ABCD-A1B1C1D1中,E,F分别为AB与BB1的中点.