题目内容
如图, 是圆
是圆 的直径,点
的直径,点 是圆
是圆 上异于
上异于 的点,直线
的点,直线
 分别为
分别为 的中点。
的中点。
(1)记平面 与平面
与平面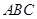 的交线为
的交线为 ,试判断
,试判断 与平面
与平面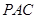 的位置关系,并加以说明;
的位置关系,并加以说明;
(2)设(1)中的直线 与圆
与圆 的另一个交点为
的另一个交点为 ,且点
,且点 满足
满足 ,记直线
,记直线
平面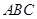 所成的角为
所成的角为 异面直线
异面直线 与
与 所成的锐角为
所成的锐角为 ,二面角
,二面角 的大小为
的大小为
①求证:
②当点 为弧
为弧 的中点时,
的中点时,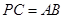 ,求直线
,求直线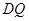 与平面
与平面 所成的角的正弦值。
所成的角的正弦值。
(1)直线 ∥平面
∥平面 (2)①详见解析②
(2)①详见解析②
解析试题分析:(1)
 面
面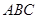 ,根据线线平行,线面平行,线与交线平行,
,根据线线平行,线面平行,线与交线平行, 从而得出线面平行,(2)①连接
从而得出线面平行,(2)①连接 ,由( 1)可知交线
,由( 1)可知交线 即为直线
即为直线 ,且
,且 ∥
∥ . 因为
. 因为 是
是 的直径,所以
的直径,所以 ,于是
,于是 .已知
.已知 平面
平面 ,而
,而 平面
平面 ,所以
,所以 .而
.而 ,所以
,所以 平面
平面 ,在不同的直角三角形内构造
,在不同的直角三角形内构造 ,做出
,做出 .③因为
.③因为 ∥
∥ ,所以直线
,所以直线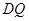 与平面
与平面 所成的角就为CF与平面
所成的角就为CF与平面 所成的角过点C作CG⊥BF,垂足为G,
所成的角过点C作CG⊥BF,垂足为G, 就是直线
就是直线 与平面
与平面 所成的角.
所成的角.
试题解析:
解(1)直线 ∥平面
∥平面 ,证明如下:连接
,证明如下:连接 ,因为
,因为 ,
, 分别是
分别是 ,
, 的中点,所以
的中点,所以 ∥
∥ . 又
. 又 平面
平面 ,且
,且 平面
平面 ,所以
,所以 ∥平面
∥平面 .而
.而 平面
平面 ,且平面
,且平面 平面
平面 ,所以
,所以 ∥
∥ . 因为
. 因为 平面
平面 ,
, 平面
平面 ,所以直线
,所以直线 ∥平面
∥平面
(2)①证明:如图,
连接 ,由(1)可知交线
,由(1)可知交线 即为直线
即为直线 ,且
,且 ∥
∥ . 因为
. 因为 是
是 的直径,所以
的直径,所以 ,于是
,于是 .
.
已知 平面
平面 ,而
,而

练习册系列答案
相关题目
 中,
中, ,G是
,G是 上的动点。
上的动点。

 ;
; 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;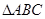 在平面
在平面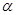 内,
内,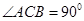 ,AB=2BC=2,P为平面
,AB=2BC=2,P为平面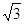 ,
,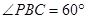
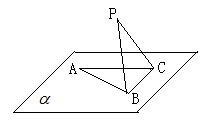
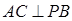
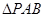 的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
的面积取得最大值时,求直线PC与平面PAB所成角的正弦值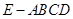 ,底面
,底面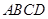 是矩形,平面
是矩形,平面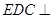 底面
底面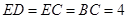 ,
,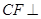 平面
平面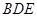 ,且点
,且点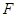 在
在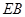 上.
上.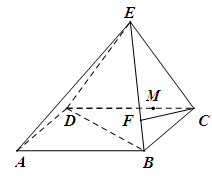
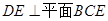 ;
;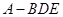 的体积;
的体积;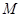 在线段
在线段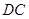 上,且满足
上,且满足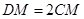 ,试在线段
,试在线段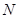 ,使得
,使得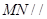 平面
平面 .
. ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
 ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
 是AC的中点,已知
是AC的中点,已知 ,
, .
.
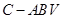 的体积.
的体积.
 中,
中,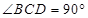 ,
,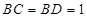 ,
, 平面
平面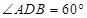 ,
, 、
、 分别是
分别是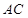 、
、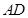 上的动点,且
上的动点,且
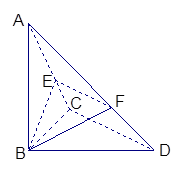
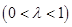 .
.
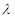 为何值,总有平面
为何值,总有平面 平面
平面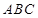 ;
; ?
?