题目内容
已知二次函数g(x)的图象经过坐标原点,且满足g(x+1)=g(x)+2x+1,设函数f(x)=mg(x)-ln(x+1),其中m为非零常数.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)若f(x)为单调减函数,求m的范围;
(Ⅲ)当m>0,x∈[0,1]时,求f(x)的最大值。
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)若f(x)为单调减函数,求m的范围;
(Ⅲ)当m>0,x∈[0,1]时,求f(x)的最大值。
解:(Ⅰ)设g(x)=ax2+bx+c,g(x)的图象经过坐标原点,所以,c=0,
∵g(x+1)=g(x)+2x+1,
∴a(x+1)2+b(x+1)=ax2+bx+2x+1,
即:ax2+(2a+b)x+a+b=ax2+(b+2)x+l,
∴a=1,b=0,g(x)=x2。
(Ⅱ)函数f(x)=mx2-ln(x+1)的定义域为(-1,+∞),
令ψ(x)=2mx2+2mx-1,
由已知f′(x)≤0在(-1,+∞)上恒成立,
即ψ(x)=2mx2+2mx-l≤0在(-1,+∞)上恒成立,
①当m>0时,不符合条件;
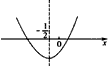
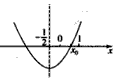
②当m<0,ψ(x)的图象如下,
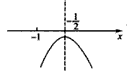
只需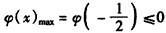 ,
,
即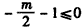 ,
,
∴m≥-2,
综上:-2≤m<0。
(Ⅲ)由已知
①ψ(1)=4m-1≤0时,即0<m≤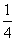 时,f(x)′≤0在[0,1]上恒成立,
时,f(x)′≤0在[0,1]上恒成立,
f(x)在[0,1]上递减,f(x)max=f(0)=0;
②当m>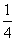 时,
时,
 ,设
,设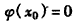 ,
,
则f(x)在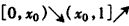 ,
,
f(0)=0,f(1)=m-ln2,
当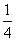 <m<ln2时,f(x)max=f(0)=0;
<m<ln2时,f(x)max=f(0)=0;
当m≥ln2时,f(x)max=f(1)=m-ln2;
综上:0<m<ln2时,f(x)max=f(0)=0;m≥ln2时,f(x)max=f(1)=m-ln2.
∵g(x+1)=g(x)+2x+1,
∴a(x+1)2+b(x+1)=ax2+bx+2x+1,
即:ax2+(2a+b)x+a+b=ax2+(b+2)x+l,
∴a=1,b=0,g(x)=x2。
(Ⅱ)函数f(x)=mx2-ln(x+1)的定义域为(-1,+∞),
令ψ(x)=2mx2+2mx-1,
由已知f′(x)≤0在(-1,+∞)上恒成立,
即ψ(x)=2mx2+2mx-l≤0在(-1,+∞)上恒成立,
①当m>0时,不符合条件;

②当m<0,ψ(x)的图象如下,

只需
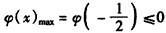 ,
,即
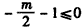 ,
,∴m≥-2,
综上:-2≤m<0。
(Ⅲ)由已知
①ψ(1)=4m-1≤0时,即0<m≤
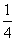 时,f(x)′≤0在[0,1]上恒成立,
时,f(x)′≤0在[0,1]上恒成立,f(x)在[0,1]上递减,f(x)max=f(0)=0;
②当m>
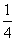 时,
时,
 ,设
,设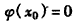 ,
,则f(x)在
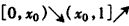 ,
,f(0)=0,f(1)=m-ln2,
当
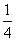 <m<ln2时,f(x)max=f(0)=0;
<m<ln2时,f(x)max=f(0)=0;当m≥ln2时,f(x)max=f(1)=m-ln2;
综上:0<m<ln2时,f(x)max=f(0)=0;m≥ln2时,f(x)max=f(1)=m-ln2.

练习册系列答案
相关题目
 )+mlnx+
)+mlnx+ (m∈R,x>0),
(m∈R,x>0),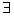 x>0使f(x)≤0成立,求实数m的取值范围;
x>0使f(x)≤0成立,求实数m的取值范围; x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1.
x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1. )+mlnx+
)+mlnx+ (m∈R),
(m∈R),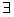 x>0使f(x)≤0成立,求实数m的取值范围;
x>0使f(x)≤0成立,求实数m的取值范围;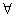 x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1。
x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1。