题目内容
下列函数中,在区间(0,+∞)上是增函数的是
- A.f(x)=-x2+2
- B.f(x)=

- C.f(x)=
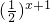
- D.f(x)=log2x
D
分析:对f(x)=-x2+2明确其开口与单调区间可判断A的正误;利用f(x)= 在(0,+∞)上是减函数,可判断B,利用,y=
在(0,+∞)上是减函数,可判断B,利用,y= 是减函数,可判断C的正误;由f(x)=log2x的单调性可判断D的正误.
是减函数,可判断C的正误;由f(x)=log2x的单调性可判断D的正误.
解答:∵f(x)=-x2+2是开口向下的抛物线,在(0,+∞)上是减函数,故A中函数不合要求;
f(x)= 在(0,+∞)上是减函数,故B中函数不合要求B;
在(0,+∞)上是减函数,故B中函数不合要求B;
∵y= 的底数0<
的底数0< <1,y=
<1,y= 是减函数,
是减函数,
∴f(x)=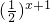 为(0,+∞)上的减函数,故C中函数不合要求;
为(0,+∞)上的减函数,故C中函数不合要求;
f(x)=log2x的底数大于1,故在区间(0,+∞)上是增函数,D中函数合乎要求.
故选D.
点评:本题考查函数单调性的判断与证明,着重考查基本初等函数的性质,属于中档题.
分析:对f(x)=-x2+2明确其开口与单调区间可判断A的正误;利用f(x)=
 在(0,+∞)上是减函数,可判断B,利用,y=
在(0,+∞)上是减函数,可判断B,利用,y= 是减函数,可判断C的正误;由f(x)=log2x的单调性可判断D的正误.
是减函数,可判断C的正误;由f(x)=log2x的单调性可判断D的正误.解答:∵f(x)=-x2+2是开口向下的抛物线,在(0,+∞)上是减函数,故A中函数不合要求;
f(x)=
 在(0,+∞)上是减函数,故B中函数不合要求B;
在(0,+∞)上是减函数,故B中函数不合要求B;∵y=
 的底数0<
的底数0< <1,y=
<1,y= 是减函数,
是减函数,∴f(x)=
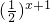 为(0,+∞)上的减函数,故C中函数不合要求;
为(0,+∞)上的减函数,故C中函数不合要求;f(x)=log2x的底数大于1,故在区间(0,+∞)上是增函数,D中函数合乎要求.
故选D.
点评:本题考查函数单调性的判断与证明,着重考查基本初等函数的性质,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
下列函数中,在区间(0,1)上是增函数的是( )
| A、y=tanx | ||
B、y=
| ||
| C、y=2-x | ||
| D、y=-x2-4x+1 |
下列函数中,在区间(0,+∞)上为减函数的是( )
A、y=log
| ||
B、y=-
| ||
| C、y=3x | ||
| D、y=1+x2 |