题目内容
2.已知直线l:ax+by+c=0及圆P:x2+y2=1,其中a,b,c满足条件:a2+b2=k2c2,其中(c≠0,k≠0)(1)试讨论直线l与圆P的位置关系,
(2)若直线l被圆P截得的弦长为1,求k的值.
分析 (1)利用点到直线的距离公式可得圆心O到直线l的距离d,通过直线l与⊙O相切?d=r?a2+b2=c2,即可判断出.
(2)利用垂径定理,通过弦长列出关系式,即可求出即可.
解答 解:(1)圆心O到直线l的距离d=$\frac{\left|c\right|}{\sqrt{{a}^{2}+{b}^{2}}}$,
直线l与⊙O相切?d=r?$\frac{\left|c\right|}{\sqrt{{a}^{2}+{b}^{2}}}$=1?a2+b2=c2,
此时k=±1,
如果k∈(-1,1),则a2+b2<c2,直线与圆的位置关系是相离;
如果k∈(-∞,-1)∪(1,+∞),则a2+b2>c2,直线与圆的位置关系是相交;
(2)直线l被圆P截得的弦长为1,可得1=2$\sqrt{1-{(\frac{\left|c\right|}{\sqrt{{a}^{2}+{b}^{2}}})}^{2}}$,
解得$\frac{{c}^{2}}{{a}^{2}+{b}^{2}}=\frac{3}{4}$,即a2+b2=$\frac{4}{3}$c2,∴k2=$\frac{4}{3}$,k=$±\frac{2\sqrt{3}}{3}$.
点评 本题考查了直线与圆相切的充要条件、直线与圆的位置关系的判定,垂径定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
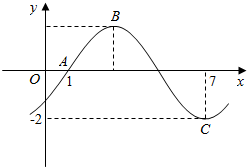 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.