��Ŀ����
�ס��ҡ�����������Ͷ��һö�ʵؾ��ȵ����������ӣ��������£����ij��ijһ������1�㣬����һ�μ����ɴ������������������������������������ץ�ξ�����˭��Ͷ�����ҵ�һ���ɼ�Ͷ�������n���ɼ�Ͷ���ĸ�����pn�����һ��Ͷ���ĸ��ʾ�Ϊqn��
��1������p1��p2��p3��ֵ��
��2��������{Pn}��ͨ�ʽ��
��3�����һ��Ͷ���У����κ�������Ͷ���ĸ���֮��ľ���ֵС��0.001����ƴ˴�Ͷ���ǡ�����ӽ����ȡ�����ô�ӵڼ���Ͷ����ʼ������ӽ����ȣ�
��1������p1��p2��p3��ֵ��
��2��������{Pn}��ͨ�ʽ��
��3�����һ��Ͷ���У����κ�������Ͷ���ĸ���֮��ľ���ֵС��0.001����ƴ˴�Ͷ���ǡ�����ӽ����ȡ�����ô�ӵڼ���Ͷ����ʼ������ӽ����ȣ�
��������1�����ݹ�����p1��p2��p3��ֵ��
��2�����n-1���ɼ�Ͷ���ĸ�����pn-1��n��2�������n-1���ɼ�Ͷ������n�����ɼ�Ͷ���ĸ�����
pn-1����n-1����������Ͷ������n���ɼ�Ͷ���ĸ�����
��
(1-pn-1)�������ɴ˿ɵ�ͨ�ʽ��
��3����qn=
����ϣ�2���Ľ��ۣ������κ�������Ͷ���ĸ���֮��ľ���ֵС��0.001����������ʽ��������ý��ۣ�
��2�����n-1���ɼ�Ͷ���ĸ�����pn-1��n��2�������n-1���ɼ�Ͷ������n�����ɼ�Ͷ���ĸ�����
| 1 |
| 6 |
| 1 |
| 2 |
| 5 |
| 6 |
��3����qn=
| 1-pn |
| 2 |
����⣺��1�������⣬p1=1��p2=
��p3=
+
��
��(1-
)=
����5�֣�
��2�����n-1���ɼ�Ͷ���ĸ�����pn-1��n��2������
��n-1���ɼ�Ͷ������n�����ɼ�Ͷ���ĸ�����
pn-1��
��n-1����������Ͷ������n���ɼ�Ͷ���ĸ�����
��
(1-pn-1)������9�֣�
����pn=
pn-1+
��
(1-pn-1)=-
pn-1+
��
���Ƶ�pn=
•(-
)n-1+
�� ����12�֣�
��3����qn=
����|pn-qn|=
��0.001����n��6
�ʴӵ�6�ο�ʼ������ӽ����ȣ�����15�֣�
| 1 |
| 6 |
| 1 |
| 36 |
| 1 |
| 2 |
| 5 |
| 6 |
| 1 |
| 6 |
| 3 |
| 8 |
��2�����n-1���ɼ�Ͷ���ĸ�����pn-1��n��2������
��n-1���ɼ�Ͷ������n�����ɼ�Ͷ���ĸ�����
| 1 |
| 6 |
��n-1����������Ͷ������n���ɼ�Ͷ���ĸ�����
| 1 |
| 2 |
| 5 |
| 6 |
����pn=
| 1 |
| 6 |
| 1 |
| 2 |
| 5 |
| 6 |
| 1 |
| 4 |
| 5 |
| 12 |
���Ƶ�pn=
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
��3����qn=
| 1-pn |
| 2 |
| 1 |
| 4n-1 |
�ʴӵ�6�ο�ʼ������ӽ����ȣ�����15�֣�
���������⿼�����֪ʶ�����ã���������ͨ���ȷ��������ѧ�������������������������е��⣮

��ϰ��ϵ�д�
 ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
�����Ŀ
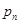 �����һ��Ͷ���ĸ��ʾ�Ϊ
�����һ��Ͷ���ĸ��ʾ�Ϊ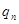 ��
��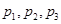 ��ֵ��
��ֵ��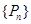 ��ͨ�ʽ��
��ͨ�ʽ��