题目内容
甲、乙、丙三人轮流投掷一枚质地均匀的正方体骰子，规则如下：如果某人某一次掷出1点，则下一次继续由此人掷，如果掷出其他点数，则另外两个人抓阄决定由谁来投掷，且第一次由甲投掷。
设第n次由甲投掷的概率是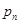
，由乙或丙投掷的概率均为
．
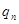（1）计算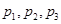
的值；
（2）求数列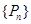
的通项公式；
（3）如果一次投掷中，由任何两个人投掷的概率之差的绝对值小于0.001，则称此次投掷是“机会接近均等”，那么从第几次投掷开始，机会接近均等？
【答案】
（1）
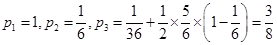
（2）
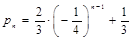
（3）从第6次开始，机会接近均等。
【解析】解：⑴易知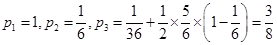………………………5分
⑵设第n-1次由甲投掷的概率是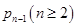
，则
第n-1次由甲投掷而第n次仍由甲投掷的概率是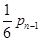
，
第n-1次由另两人投掷而第n次由甲投掷的概率是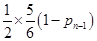
， ……………9分
于是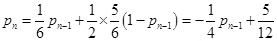
，
递推得。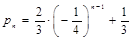
……………………12分
（3）由
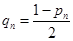，得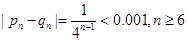
故从第6次开始，机会接近均等。 ………………………15分
练习册系列答案
相关题目
、
、
。