题目内容
已知函数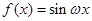
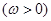 在区间
在区间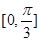 上单调递增,在区间
上单调递增,在区间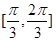 上单调递减;如图,四边形
上单调递减;如图,四边形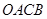 中,
中, ,
, ,
, 为
为 的内角
的内角 的对边,
的对边,
且满足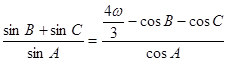 .
.
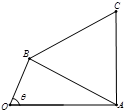
(Ⅰ)证明: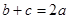 ;
;
(Ⅱ)若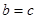 ,设
,设 ,
, ,
,
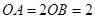 ,求四边形
,求四边形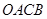 面积的最大值.
面积的最大值.
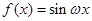
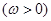 在区间
在区间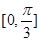 上单调递增,在区间
上单调递增,在区间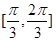 上单调递减;如图,四边形
上单调递减;如图,四边形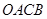 中,
中,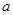 ,
,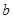 ,
,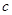 为
为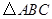 的内角
的内角 的对边,
的对边,且满足
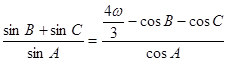 .
.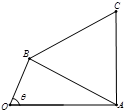
(Ⅰ)证明:
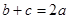 ;
;(Ⅱ)若
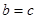 ,设
,设 ,
, ,
,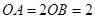 ,求四边形
,求四边形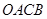 面积的最大值.
面积的最大值.(1)正弦定理的运用根据边角的转换来得到证明。
(2)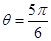 时取最大值,
时取最大值,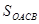 的最大值为
的最大值为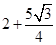
(2)
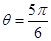 时取最大值,
时取最大值,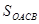 的最大值为
的最大值为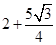
试题分析:解:(Ⅰ)由题意知:
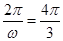 ,解得:
,解得: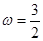 , 2分
, 2分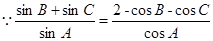
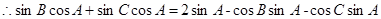
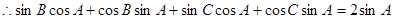
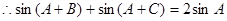 4分
4分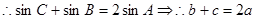 6分
6分(Ⅱ)因为
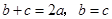 ,所以
,所以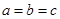 ,所以
,所以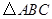 为等边三角形
为等边三角形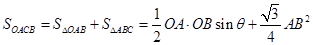 8分
8分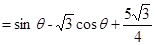
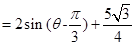 , 10分
, 10分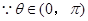 ,
,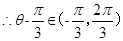 ,
, 当且仅当
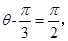 即
即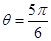 时取最大值,
时取最大值,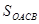 的最大值为
的最大值为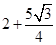 12分
12分点评:解决的关键是利用三角函数的性质得到最值,属于基础题。

练习册系列答案
相关题目
 ,行驶4h后,船到达C处,看到这个灯塔在北偏东
,行驶4h后,船到达C处,看到这个灯塔在北偏东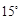 ,这时船与灯塔的距离为 km.
,这时船与灯塔的距离为 km. 中角A、B、C的对边分别是a、b、c,
中角A、B、C的对边分别是a、b、c, ,则三角形是( )
,则三角形是( )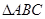 中,
中,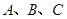 的对边分别为
的对边分别为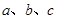 ,且
,且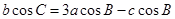 .
. 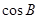 的值;
的值;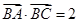 ,
,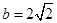 ,求
,求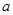 和
和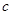 .
.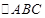 中,边
中,边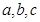 所对的角分别为
所对的角分别为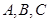 ,若
,若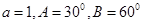 ,则
,则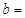 ( )
( )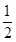
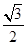
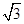
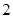
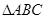 中,
中,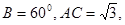 则AB+3BC的最大值为 .
则AB+3BC的最大值为 . 满足
满足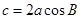 ,则
,则