题目内容
(不等式选讲)若实数x,y,z满足x2+y2+z2=9,则x+2y+3z的最大值是______.
由柯西不等式可得:(x2+y2+z2)×(12+22+32)≥(x+2y+3z)2
已知x2+y2+z2=9,
∴(x+2y+3z)2≤9×14,
∴x+2y+3z的最大值是3
.
故答案为:3
.
已知x2+y2+z2=9,
∴(x+2y+3z)2≤9×14,
∴x+2y+3z的最大值是3
| 14 |
故答案为:3
| 14 |

练习册系列答案
相关题目
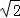 .M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
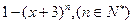 能被
能被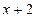 整除
整除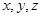 ,
,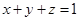 ,求证:
,求证: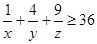 ;
;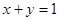 ,求
,求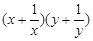 的最小值。
的最小值。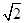 ,高SE=8,则过点A,B,C,D,S的球的半径为( )
,高SE=8,则过点A,B,C,D,S的球的半径为( )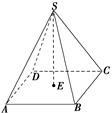
 为正四面体
为正四面体 表面(含棱)上与顶点不重合的一点,由点
表面(含棱)上与顶点不重合的一点,由点 ,如果集合
,如果集合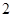 个元素,那么符合条件的点
个元素,那么符合条件的点

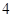 个
个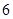 个
个 个
个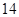 个
个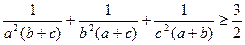 .
.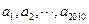 都为正数,且
都为正数,且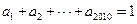 ,则
,则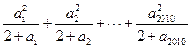 的最小值是 .
的最小值是 .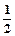 x2-1恒成立,求实数a的取值范围。
x2-1恒成立,求实数a的取值范围。