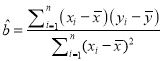题目内容
【题目】已知函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,即
,即![]() ,若
,若![]() ,则称
,则称![]() 在
在![]() 上封闭.
上封闭.
(1)分别判断函数![]() ,
, ![]() 在
在![]() 上是否封闭,说明理由;
上是否封闭,说明理由;
(2)函数![]() 的定义域为
的定义域为![]() ,且存在反函数
,且存在反函数![]() ,若函数
,若函数![]() 在
在![]() 上封闭,且函数
上封闭,且函数![]() 在
在![]() 上也封闭,求实数
上也封闭,求实数![]() 的取值范围;
的取值范围;
(3)已知函数![]() 的定义域为
的定义域为![]() ,对任意
,对任意![]() ,若
,若![]() ,有
,有![]() 恒成立,则称
恒成立,则称![]() 在
在![]() 上是单射,已知函数
上是单射,已知函数![]() 在
在![]() 上封闭且单射,并且满足
上封闭且单射,并且满足![]()
![]() ,其中
,其中![]() (
(![]() ),
),![]() ,证明:存在
,证明:存在![]() 的真子集,
的真子集, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,使得
,使得![]() 在所有
在所有![]() (
(![]() )上封闭.
)上封闭.
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)根据![]() 在
在![]() 上封闭的定义,分别求出函数
上封闭的定义,分别求出函数![]() ,
, ![]() 在
在![]() 上的值域,即可判断是否封闭;(2)函数
上的值域,即可判断是否封闭;(2)函数![]() 在D上封闭,则
在D上封闭,则![]() .函数
.函数![]() 在
在![]() 上封闭,则
上封闭,则![]() ,得到:
,得到: ![]() .从而问题转化为:
.从而问题转化为: ![]() 在
在![]() 两不等实根.(3)分两种情况:
两不等实根.(3)分两种情况: ![]() 和
和![]() ,第一种情况显然不成立,第二种情况,因为
,第一种情况显然不成立,第二种情况,因为![]() 是单射,因此取一个
是单射,因此取一个![]() ,则
,则![]() 是唯一的使得
是唯一的使得![]() 的根,换句话说
的根,换句话说![]() 考虑到
考虑到![]() ,即
,即![]() ,因为
,因为![]() 是单射,则
是单射,则![]() 这样就有了
这样就有了![]() .接着令
.接着令![]() ,并重复上述论证证明
,并重复上述论证证明![]() ..
..
试题解析:
(1)因为函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,(取一个具体例子也可),
,(取一个具体例子也可),
所以![]() 在
在![]() 上不封闭.
上不封闭.
![]()
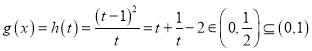
![]() 在
在![]() 上封闭
上封闭
(2)函数![]() 在D上封闭,则
在D上封闭,则![]() .函数
.函数![]() 在
在![]() 上封闭,则
上封闭,则![]() ,
,
得到: ![]() .
.
![]() 在
在![]() 单调递增.
单调递增.
则![]()
![]() 在
在![]() 两不等实根.
两不等实根.
![]() ,
,
故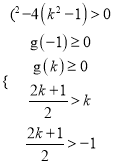 ,解得
,解得![]() .
.
另解: ![]() 在
在![]() 两不等实根.令
两不等实根.令![]()
![]() 在
在![]() 有两个不等根,画图,由数形结合可知,
有两个不等根,画图,由数形结合可知, ![]()
解得![]() .
.
(3)如果![]() ,则
,则![]() ,与题干
,与题干![]() 矛盾.
矛盾.
因此![]() ,取
,取![]() ,则
,则![]() .
.
接下来证明![]() ,因为
,因为![]() 是单射,因此取一个
是单射,因此取一个![]() ,
,
则![]() 是唯一的使得
是唯一的使得![]() 的根,换句话说
的根,换句话说![]()
考虑到![]() ,即
,即![]() ,
,
因为![]() 是单射,则
是单射,则![]()
这样就有了![]() .
.
接着令![]() ,并重复上述论证证明
,并重复上述论证证明![]() ..
..

 每日10分钟口算心算速算天天练系列答案
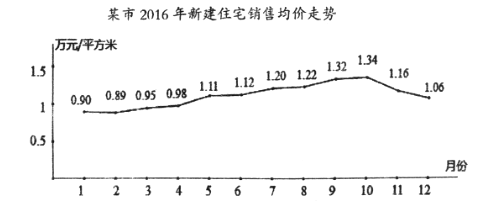
每日10分钟口算心算速算天天练系列答案【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从中国某城市的高中生中,随机抽取了55人,从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是:选择家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .美国高中生答题情况是:家占
.美国高中生答题情况是:家占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .为了考察高中生的“恋家(在家里感到最幸福)”是否与国别有关,构建了如下
.为了考察高中生的“恋家(在家里感到最幸福)”是否与国别有关,构建了如下![]() 列联表.
列联表.
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
(Ⅰ)请将![]() 列联表补充完整;试判断能否有
列联表补充完整;试判断能否有![]() 的把握认为“恋家”与否与国别有关;
的把握认为“恋家”与否与国别有关;
(Ⅱ)从中国高中生的学生中以“是否恋家”为标准采用分层抽样的方法,随机抽取了5人,再从这5人中随机抽取2人.若所选2名学生中的“恋家”人数为![]() ,求随机变量
,求随机变量![]() 的分布列及期望.
的分布列及期望.
附: 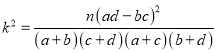 ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |