题目内容
设数列{an}的前项和为Sn,已知a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N*).
(1)求a1,a2的值;
(2)求证:数列{Sn+2}是等比数列;
(3)抽去数列{an}中的第1项,第4项,第7项,……,第3n-2项,……,余下的项顺序不变,组成一个新数列{bn},若{bn}的前n项的和为Tn,求证:![]() .
.
答案:
解析:
解析:
|
(1) (2) 由①-②,得 所以 (3)由(2)得 抽去数列 所以当 当 综上, |

练习册系列答案
相关题目
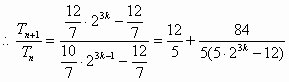
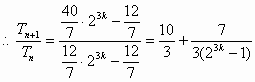
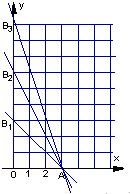 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组