题目内容
设数列{an}的前项和为Sn,且对任意正整数,an+Sn=4096,(注:1024=210,2048=211,4096=212).
(1)求数列{an}的通项公式;
(2)设数列{log2an}的前项和为Tn,对数列{Tn},从第几项起Tn≤-165?
(1)求数列{an}的通项公式;
(2)设数列{log2an}的前项和为Tn,对数列{Tn},从第几项起Tn≤-165?
分析:(1)由an+Sn=4096,知a1+S1=4096,a1=2048.当n≥2时,an=Sn-Sn-1=an-1-an,由此能求出数列{an}的通项公式.
(2)由log2an=log2[2048(
)n-1]=12-n,知Tn=
(-n2+23n).由此能求出从第几项起Tn≤-165.
(2)由log2an=log2[2048(
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵an+Sn=4096,
∴a1+S1=4096,
a1=2048.
当n≥2时,an=Sn-Sn-1=(4096-an)-(4096-an-1)=an-1-an
∴
=
,
∴an=2048(
)n-1.
(2)∵log2an=log2[2048(
)n-1]=12-n,
∴Tn=
(-n2+23n).
由Tn≤-165,
解得n≥33,
故从第33项起,Tn≤-165.
∴a1+S1=4096,
a1=2048.
当n≥2时,an=Sn-Sn-1=(4096-an)-(4096-an-1)=an-1-an
∴
| an |
| an-1 |
| 1 |
| 2 |
∴an=2048(
| 1 |
| 2 |
(2)∵log2an=log2[2048(
| 1 |
| 2 |
∴Tn=
| 1 |
| 2 |
由Tn≤-165,
解得n≥33,
故从第33项起,Tn≤-165.
点评:本题考查函数与数列的综合,是中档题.解题时要认真审题,注意数列的通项公式的求法和数列前n项和公式的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
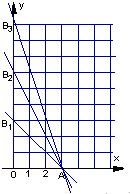 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组