题目内容
【题目】已知函数f(x)=(x﹣1)2﹣alnx(a<0).
(1)讨论f(x)的单调性;
(2)若f(x)存在两个极值点x1,x2(x1<x2),且关于x的方程f(x)=b(b∈R)恰有三个实数根x3,x4,x5(x3<x4<x5),求证:2(x2﹣x1)>x5﹣x3.
【答案】(1)答案不唯一,具体见解析(2)证明见解析
【解析】
(1)求导得f′(x)![]() ,令f′(x)=0,即2x2﹣2x﹣a=0,
,令f′(x)=0,即2x2﹣2x﹣a=0,![]() =4+8a,分两种情况①
=4+8a,分两种情况①![]() ≤0,②
≤0,②![]() >0,讨论f(x)单调性;
>0,讨论f(x)单调性;
(2)由题意得![]() a<0,画出草图,知0<x3<x1<x4<x2<x5,0<x1<x2<1,要证:2(x2﹣x1)>x5﹣x3,即证:2(x2﹣x1)>(x5+x4)﹣(x3+x4),只需证:
a<0,画出草图,知0<x3<x1<x4<x2<x5,0<x1<x2<1,要证:2(x2﹣x1)>x5﹣x3,即证:2(x2﹣x1)>(x5+x4)﹣(x3+x4),只需证: ,先证:x3+x4>2x1.即证x4>2x1﹣x3,由(1)f(x)单调递减,只需证f(x4)<f(2x1﹣x3),即证:f(x3)<f(2x1﹣x3),令g(x)=f(x)﹣f(2x1﹣x),0<x<x1,求导数,分析单调性,可得g(x)<g(x1)=0,故f(x)<f(2x1﹣x),在(0,x1)恒成立,f(x3)<f(2x1﹣x3)得证,同理可以证明:x3+x4<2x2,综上,2(x2﹣x1)>x5﹣x3,得证.
,先证:x3+x4>2x1.即证x4>2x1﹣x3,由(1)f(x)单调递减,只需证f(x4)<f(2x1﹣x3),即证:f(x3)<f(2x1﹣x3),令g(x)=f(x)﹣f(2x1﹣x),0<x<x1,求导数,分析单调性,可得g(x)<g(x1)=0,故f(x)<f(2x1﹣x),在(0,x1)恒成立,f(x3)<f(2x1﹣x3)得证,同理可以证明:x3+x4<2x2,综上,2(x2﹣x1)>x5﹣x3,得证.
(1)由题意得![]() =2(x﹣1)
=2(x﹣1)![]() ,
,
令![]() =0,即2x2﹣2x﹣a=0,
=0,即2x2﹣2x﹣a=0,![]() =4+8a,
=4+8a,
①当a![]() 时,
时,![]() ≤0,
≤0,![]() ≥0,函数f(x)在(0,+∞)上单调递增,
≥0,函数f(x)在(0,+∞)上单调递增,
②当![]() a<0时,
a<0时,![]() >0,
>0,
2x2﹣2x﹣a=0的两根为x1![]() ,x2
,x2![]() 且0<x1
且0<x1![]() x2,
x2,
当x∈(0,![]() ),(
),(![]() ,+∞)时,
,+∞)时,![]() >0,f(x)单调递增,
>0,f(x)单调递增,
当x∈(![]() ,
,![]() )时,
)时,![]() <0,f(x)单调递减,
<0,f(x)单调递减,
综上,当a![]() 时,函数f(x)在(0,+∞)上单调递增,
时,函数f(x)在(0,+∞)上单调递增,
当![]() a<0时,f(x)在(0,
a<0时,f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,
,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
(2)证明:由题意得![]() a<0,0<x3<x1<x4<x2<x5,0<x1<x2<1,如图,
a<0,0<x3<x1<x4<x2<x5,0<x1<x2<1,如图,
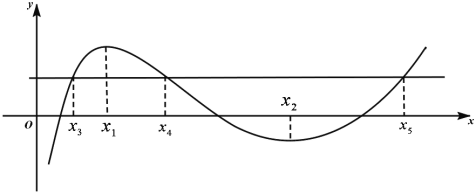
要证:2(x2﹣x1)>x5﹣x3,
即证:2(x2﹣x1)>(x5+x4)﹣(x3+x4);
只需证:
先证:x3+x4>2x1.
即证x4>2x1﹣x3,
又由(1)知f(x)在(x1,x2)上单调递减,
只需证f(x4)<f(2x1﹣x3),
而f(x4)=f(x3),即证:f(x3)<f(2x1﹣x3),
令g(x)=f(x)﹣f(2x1﹣x),0<x<x1,
![]() =
=![]() +
+![]() =2x﹣2
=2x﹣2![]() 2(2x1﹣x)﹣2
2(2x1﹣x)﹣2![]() ,
,
=4(x1﹣1)![]()
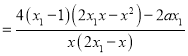
又2(x1﹣1)![]() 0,即x1﹣1
0,即x1﹣1![]() ,那么,
,那么,
![]()
 ,而0<x<x1,且
,而0<x<x1,且![]() ,
,
则![]() >0,故g(x)在(0,x1)单调递增,则g(x)<g(x1)=0,
>0,故g(x)在(0,x1)单调递增,则g(x)<g(x1)=0,
故f(x)<f(2x1﹣x),在(0,x1)恒成立,
又0<x3<x1,则f(x3)<f(2x1﹣x3)得证,
同理可以证明:x3+x4<2x2,
综上,2(x2﹣x1)>x5﹣x3,得证.

【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量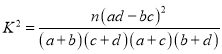 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |