题目内容
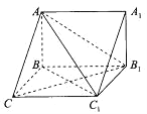
【题目】如图,在三棱柱![]() 侧面
侧面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)要证平面![]() 平面
平面![]() ,转证
,转证![]() 平面AB
平面AB![]() ,即证
,即证![]() ,
,![]() ;
;
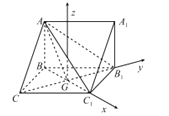
(2) 以G为坐标原点,以![]() 的方向为x轴正方向,以
的方向为x轴正方向,以![]() 的方向为y轴正方向,建立如图所示的空间直角坐标系G-xyz.分别求出两个半平面的法向量,代入公式即可得到结果.
的方向为y轴正方向,建立如图所示的空间直角坐标系G-xyz.分别求出两个半平面的法向量,代入公式即可得到结果.
(1)如图,设![]() ,连接AG.
,连接AG.
因为三棱柱的侧面![]() 为平行四边形,所以G为
为平行四边形,所以G为![]() 的中点,
的中点,
因为![]() ,
,
所以![]() 为等腰三角形,所以
为等腰三角形,所以![]() ,
,
又因为AB⊥侧面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]()
又因为![]() ,
,
所以![]() 平面AB
平面AB![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ;
;
(2)由(1)知![]() 平面AB
平面AB![]() ,所以
,所以![]() B
B![]()
以G为坐标原点,以![]() 的方向为x轴正方向,以
的方向为x轴正方向,以![]() 的方向为y轴正方向,建立如图所示的空间直角坐标系G-xyz.
的方向为y轴正方向,建立如图所示的空间直角坐标系G-xyz.
由![]() B
B![]() 易知四边形
易知四边形![]() 为菱形,因为
为菱形,因为![]()
所以![]() ,
,
则可得![]() ,
,
所以![]()
设平面![]() 的法向量
的法向量![]() ,
,
由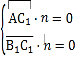 得:
得:![]() ,取z=1,所以
,取z=1,所以![]() ,
,
由(1)知![]() =
=![]() 为平面AB
为平面AB![]() 的法向量,
的法向量,
则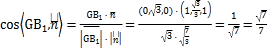
易知二面角![]() 的余弦值
的余弦值![]() .
.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案【题目】阿尔法狗(AlphaGo)是第一个击败人类职业围棋选手、第一个战胜围棋世界冠军的人工智能程序,由谷歌(Google)公司的团队开发.其主要工作原理是“深度学习”.2017 年5 月,在中国乌镇围棋峰会上,它与排名世界第一的世界围棋冠军柯洁对战,以3 比0 的总比分获胜.围棋界公认阿尔法围棋的棋力已经超过人类职业围棋顶尖水平.
为了激发广大中学生对人工智能的兴趣,某市教育局组织了一次全市中学生“人工智能”软件设计竞赛,从参加比赛的学生中随机抽取了30 名学生,并把他们的比赛成绩按五个等级进行了统计,得到如下数据表:
成绩等级 |
|
|
|
|
|
成绩(分) | 5 | 4 | 3 | 2 | 1 |
人数(名) | 4 | 6 | 10 | 7 | 3 |
(1)根据上面的统计数据,试估计从本市参加比赛的学生中任意抽取一人,其成绩等级为“![]() 或
或![]() ”的
”的
概率;
(2)根据(I)的结论,若从该地区参加比赛的学生(参赛人数很多)中任选3 人,记![]() 表示抽到成绩等级为“
表示抽到成绩等级为“![]() 或
或![]() ”的学生人数,求
”的学生人数,求![]() 的分布列及其数学期望
的分布列及其数学期望![]() ;
;
(3)从这30 名学生中,随机选取2 人,求“这两个人的成绩之差大于1分”的概率.
【题目】某烘焙店加工一个成本为60元的蛋糕,然后以每个120元的价格出售,如果当天卖不完,剩下的这种蛋糕作餐厨垃圾处理.
(1)若烘焙店一天加工16个这种蛋糕,,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)烘焙店记录了100天这种蛋糕的日需求量(单位:个),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①若烘焙店一天加工16个这种蛋糕,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列与数学期望及方差;
的分布列与数学期望及方差;
②若烘焙店一天加工16个或17个这种蛋糕,仅从获得利润大的角度考虑,你认为应加工16个还是17个?请说明理由.