题目内容
如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米建立适当的直角坐标系,求抛物线方程.
现将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少? 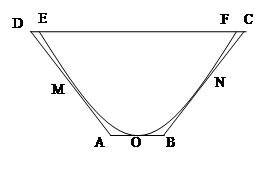
(1)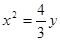 (2)梯形ABCD的下底AB=
(2)梯形ABCD的下底AB=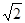 米时,所挖的土最少.
米时,所挖的土最少.
解析试题分析:(1)如图 以O为原点,AB所在的直线
为X轴,建立平面直角坐标系, 1分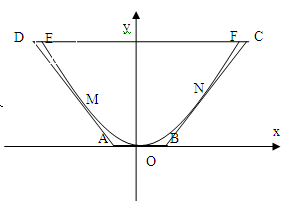
则F(2,3), 2分
设抛物线的方程是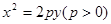 3分
3分
因为点F在抛物线上,所以
所以抛物线的方程是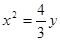 5分
5分
(2) 依题等腰梯形ABCD中,AB∥CD,线段AB的中点O是抛物线的顶点,AD,AB,BC分别与抛物线切于点M,O,N 6分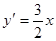 ,设
,设 ,
,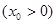 ,则抛物线在N处的切线方程是
,则抛物线在N处的切线方程是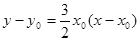 ,且
,且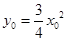 8分
8分
所以 , 10分
, 10分
梯形ABCD的面积是 12分
12分
答:梯形ABCD的下底AB=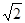 米时,所挖的土最少.
米时,所挖的土最少.
考点:本题考查了抛物线的实际运用
点评:借助坐标系,将实际应用问题、几何问题转化代数计算问题,这是解析几何的任务之一.

练习册系列答案
相关题目
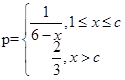 (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.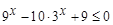 ,求函数
,求函数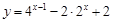 的最大值和最小值;
的最大值和最小值; 在
在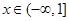 上f (x)
上f (x)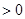 恒成立,求a的取值范围.
恒成立,求a的取值范围.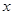 (件)之间近似满足关系:
(件)之间近似满足关系: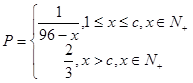 (其中
(其中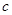 为小于96的正整常数)
为小于96的正整常数) ,如P=0.1表示每生产10件产品,有1件次品,其余为合格品.)已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损A/2元,故厂方希望定出合适的日产量。
,如P=0.1表示每生产10件产品,有1件次品,其余为合格品.)已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损A/2元,故厂方希望定出合适的日产量。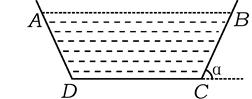
 (2)
(2)
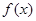 是定义在
是定义在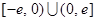 上的奇函数,当
上的奇函数,当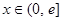 时,有
时,有 (其中
(其中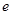 为自然对数的底,
为自然对数的底,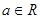 ).
).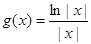 ,
,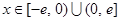 ,求证:当
,求证:当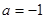 时,
时,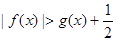 ;
; ,使得当
,使得当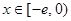 时,
时,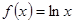 ,
,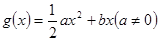
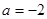 时,
时,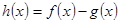 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围; 的图象
的图象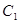 与函数
与函数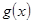 的图象
的图象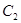 交于
交于 ,
,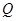 两点,过线段
两点,过线段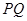 的中点
的中点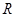 作
作 轴的垂线分别交
轴的垂线分别交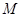 ,
, ,问是否存在点
,问是否存在点