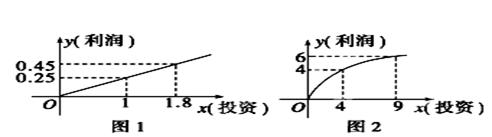
题目内容
某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系: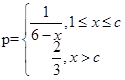 (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
(1)T=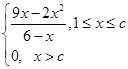 ;
;
(2)当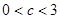 时,日产量为c万件时,可获得最大利润,当
时,日产量为c万件时,可获得最大利润,当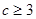 时,日产量为3万件时,可获得最大利润
时,日产量为3万件时,可获得最大利润
解析试题分析:解:(1)当x>c时,P=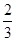 ,则T=
,则T=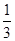 x×2-
x×2-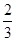 x×1=0. 当1≤x≤c时,P=
x×1=0. 当1≤x≤c时,P=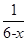 , 则T=(1-
, 则T=(1-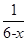 )x×2-(
)x×2-(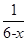 )x×1=
)x×1=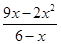 . 综上,日盈利额T(万元)与日产量x(万件)的函数关系为: T=
. 综上,日盈利额T(万元)与日产量x(万件)的函数关系为: T=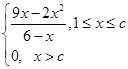 ; (2)由(1)知,当x>c时,每天的盈利额为0. 当1≤x≤c时,T=
; (2)由(1)知,当x>c时,每天的盈利额为0. 当1≤x≤c时,T=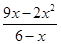 =15-2[(6-x)+
=15-2[(6-x)+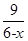 ].因c为小于6的正常数,故6-x>0,故T=15-2[(6-x)+
].因c为小于6的正常数,故6-x>0,故T=15-2[(6-x)+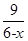 ]≤15-12=3, 当且仅当x=3时取等号. 综上,当
]≤15-12=3, 当且仅当x=3时取等号. 综上,当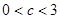 时,日产量为c万件时,可获得最大利润,当
时,日产量为c万件时,可获得最大利润,当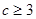 时,日产量为3万件时,可获得最大利润.
时,日产量为3万件时,可获得最大利润.
考点:函数模型的运用
点评:主要是考查了分段函数的实际运用,求解函数的最值,属于中档题。

练习册系列答案
相关题目
 千件,需另投入成本为
千件,需另投入成本为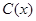 ,当年产量不足80千件时,
,当年产量不足80千件时,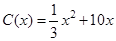 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,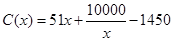 (万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.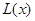 (万元)关于年产量
(万元)关于年产量 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米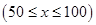 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油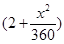 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.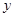 关于
关于 与时间
与时间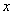 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: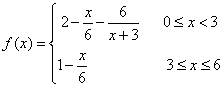 ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于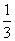 时,才能对污
时,才能对污 ,求
,求