题目内容
具有相同定义域D的函数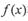 和,
和,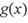 ,若对任意的
,若对任意的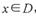 ,都有
,都有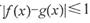 ,则称
,则称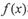 和
和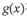 在D上是“密切函数”.给出定义域均为
在D上是“密切函数”.给出定义域均为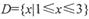 的四组函数:、
的四组函数:、
①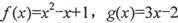
②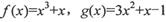
③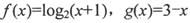
④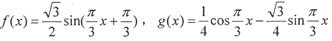
其中,函数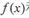 与
与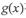 在D上为“密切函数”的是_______.
在D上为“密切函数”的是_______.
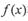 和,
和,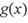 ,若对任意的
,若对任意的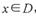 ,都有
,都有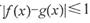 ,则称
,则称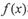 和
和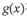 在D上是“密切函数”.给出定义域均为
在D上是“密切函数”.给出定义域均为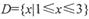 的四组函数:、
的四组函数:、①
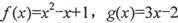
②
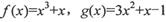
③
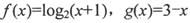
④
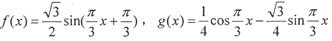
其中,函数
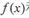 与
与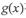 在D上为“密切函数”的是_______.
在D上为“密切函数”的是_______.①④
试题分析:①f(x)=x2-x+1,g(x)=3x-2
设h(x)=f(x)-g(x)=x2-4x+3
h(x)在[1,2]上单调减,在[2,3]上单调增
∴h(x)的最大值为0,最小值为-1
∴对任意的x∈[1,3],都有|f(x)-g(x)|≤1,符合定义
②f(x)=x3+x,g(x)=3x2+x-1
设h(x)=f(x)-g(x)=x3+3x2+1
h′(x)=3x2+6x,x∈[1,3],h′(x)>0
h(x)在[1,3]上单调增
∴h(x)的最大值为55,最小值为5,
∴对任意的x∈[1,3],|f(x)-g(x)|≤1不成立,不符合定义
③f(x)=log2(x+1),g(x)=3-x
设h(x)=f(x)-g(x)=log2(x+1)+x-3
h(x)在[1,3]上单调增
∴h(x)的最大值为2,最小值为-1,
∴对任意的x∈[1,3],|f(x)-g(x)|≤1不成立,不符合定义
④
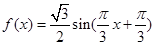 ,
, 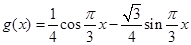
设h(x)=f(x)-g(x)=
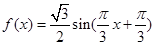 -(
-(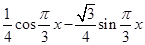 )=
)=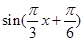
∵x∈[1,3],∴
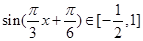
∴对任意的x∈[1,3],都有|f(x)-g(x)|≤1,符合定义
故答案为:①④
点评:解决该试题的关键是对照新定义,构造新函数h(x)=f(x)-g(x),利用导数的方法确定函数的单调性,从而确定函数的值域,利用若对任意的x∈D,都有|f(x)-g(x)|≤1,则称f(x)和g(x)在D上是“密切函数”,即可得到结论

练习册系列答案
相关题目
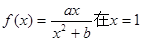 处取得极值2。
处取得极值2。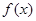 的解析式;
的解析式; 为增函数;
为增函数;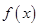 是偶函数,且
是偶函数,且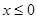 时,
时,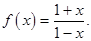 。
。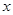 >0时
>0时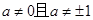 ,证明:
,证明: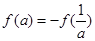
 ”:
”: ,
, ,则函数
,则函数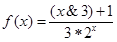
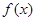 对于其定义域内的某一数
对于其定义域内的某一数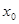 ,有
,有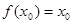 ,则称
,则称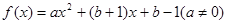 .
.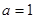 ,
, 时,求函数
时,求函数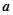 的取值范围;
的取值范围;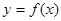 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数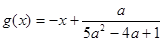 的图象上,求实数b的最小值.
的图象上,求实数b的最小值.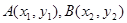 ,则线段AB的中点坐标为
,则线段AB的中点坐标为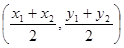 )
)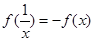 的函数,我们称为满足“倒负”变换的函数,下列函数:①
的函数,我们称为满足“倒负”变换的函数,下列函数:①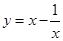 ;②
;②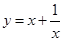 ;③
;③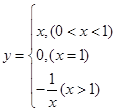 中满足“倒负”变换的函数是( )
中满足“倒负”变换的函数是( )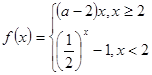 是R是的单调递减函数,则实数
是R是的单调递减函数,则实数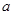 的取值范围是( )
的取值范围是( )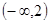
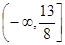
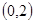
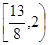
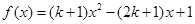 ,
, .
.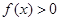 恒成立,求实数
恒成立,求实数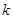 的取值范围;
的取值范围;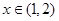 时,
时,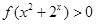 恒成立,求实数
恒成立,求实数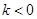 时,解不等式
时,解不等式