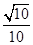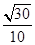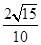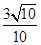题目内容
如图所示,在棱长为1的正方体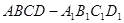 的面对角线
的面对角线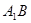 上存在一点
上存在一点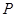 使得
使得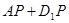 最短,则
最短,则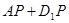 的最小值为( )
的最小值为( )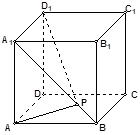
A.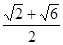 | B.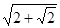 | C.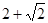 | D.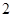 |
B
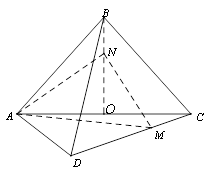
解析试题分析:如图所示,把对角面A1C绕A1B旋转至A1BC′D1′,
使其与△AA1B在同一平面上,连接AD1′,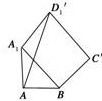
则AD1′=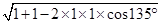 =
=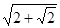 为所求的最小值.故选B.
为所求的最小值.故选B.
考点:正方体的几何特征,余弦定理的应用。
点评:中档题,将空间问题转化成平面问题,是解答立体几何问题的一种常见思路。本题利用对称性,在三角形中应用余弦定理,凸显所学知识应用的灵活性。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
用 、
、 、
、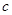 表示三条不同的直线,
表示三条不同的直线,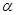 表示平面,给出下列命题:
表示平面,给出下列命题:
①若 ∥
∥ ,
, ∥
∥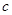 ,则
,则 ∥
∥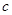 ; ②若
; ②若 ⊥
⊥ ,
, ⊥
⊥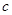 ,则
,则 ⊥
⊥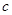 ;
;
③若 ∥
∥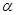 ,
, ∥
∥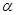 ,则
,则 ∥
∥ ; ④若
; ④若 ⊥
⊥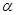 ,
, ⊥
⊥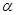 ,则
,则 ∥
∥ .
.
| A.①② | B.②③ | C.①④ | D.③④ |
已知 ,则线段
,则线段 的中点
的中点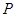 的坐标为 ( )
的坐标为 ( )
A.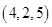 | B. | C.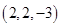 | D.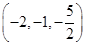 |
已知 是不同的两条直线,
是不同的两条直线,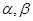 是不重合的两个平面,则下列命题中为真命题的是( )
是不重合的两个平面,则下列命题中为真命题的是( )
A.若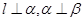 ,则 ,则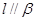 |
B.若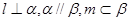 ,则 ,则 |
C.若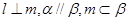 ,则 ,则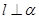 |
D.若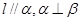 ,则 ,则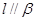 |
已知直线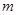 、
、 、
、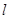 不重合,平面
不重合,平面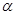 、
、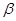 不重合,下列命题正确的是( )
不重合,下列命题正确的是( )
A.若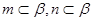 , ,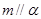 , ,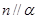 ,则 ,则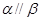 |
B.若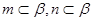 , ,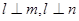 ,则 ,则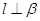 |
C.若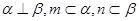 ,则 ,则 |
D.若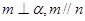 ,则 ,则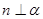 |
在棱长为2的正方体中,点E,F分别是棱AB,BC的中点,则点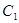 到平面
到平面 的距离等于( )
的距离等于( )
A.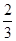 | B.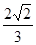 | C.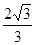 | D. |
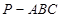 中,
中,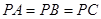 ,底面
,底面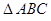 是正三角形,
是正三角形,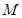 、
、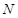 分别是侧棱
分别是侧棱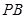 、
、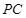 的中点. 若平面
的中点. 若平面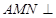 平面
平面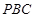 ,则侧棱
,则侧棱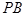 与平面
与平面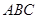 所成角的正切值是( )
所成角的正切值是( )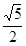
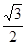
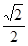
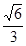
 的边长为
的边长为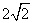 ,将
,将 沿对角线
沿对角线 折起,使平面
折起,使平面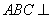 平面
平面 ,得到如图所示的三棱锥
,得到如图所示的三棱锥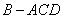 .若
.若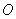 为
为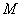 ,
, 分别为线段
分别为线段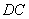 ,
,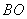 上的动点(不包括端点),且
上的动点(不包括端点),且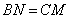 .设
.设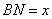 ,则三棱锥
,则三棱锥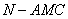 的体积
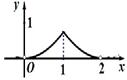
的体积 的函数图象大致是
的函数图象大致是