题目内容
长方体ABCDA1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为
A.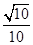 | B.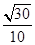 | C.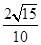 | D.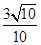 |
B
解析试题分析:建立坐标系如图.则A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2).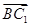 =(-1,0,2),
=(-1,0,2),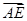 =(-1,2,1),
=(-1,2,1),
所以cos<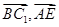 >═
>═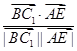 =
=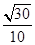 .
.
所以异面直线BC1与AE所成角的余弦值为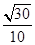 .
.
故选B。
考点:本题主要考查正方体几何特征,角的计算。
点评:简单题,正方体具备了建立空间直角坐标系的“天然条件”,因此,利用空间向量解题较为方便。

练习册系列答案
相关题目
如图,在正方体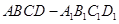 中,
中,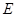 、
、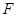 分别为棱
分别为棱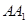 、
、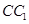 的中点,则在空间中与直线
的中点,则在空间中与直线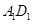 、
、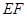 、CD都相交的直线有
、CD都相交的直线有
| A.1条 | B.2条 | C.3条 | D.无数条 |
a,b,c表示三条不重合的直线,M表示平面,给出下列四个命题:①若a∥M,b∥M,则a∥b;②若b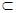 M,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有
M,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有
| A.0个 | B.1个 | C.2个 | D.3个 |
如图,在长方体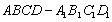 中,
中, ,
, ,则异面直线
,则异面直线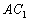 与
与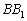 所成的角为 ( )
所成的角为 ( )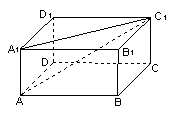
A.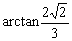 | B. | C.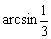 | D.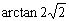 |
如图所示,正方体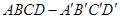 的棱长为1,O是平面
的棱长为1,O是平面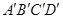 的中心,则O到平面
的中心,则O到平面 的距离是( )
的距离是( )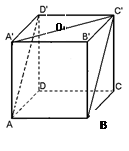
A. | B.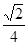 | C.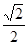 | D.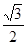 |
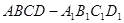 的面对角线
的面对角线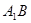 上存在一点
上存在一点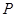 使得
使得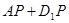 最短,则
最短,则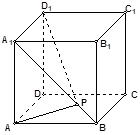
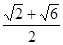
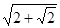
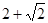
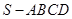 的底面边长为
的底面边长为 ,高
,高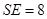 ,点
,点 在高
在高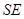 上,且
上,且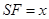 ,记过点
,记过点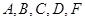 的球的半径为
的球的半径为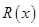 ,则函数
,则函数
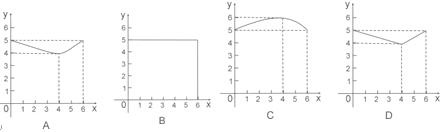
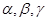 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: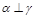 ,
,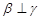 ,则
,则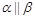 ;
;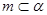 ,
,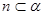 ,
,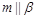 ,
,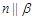 ,则
,则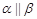 ;
;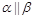 ,
,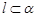 ,则
,则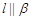 ;
;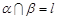 ,
,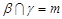 ,
,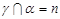 ,
,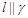 ,则
,则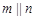 其中真命
其中真命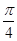 和
和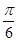 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )
,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )