题目内容
设 ,且方程
,且方程 有两个不同的实数根,则这两个实根的和为 .
有两个不同的实数根,则这两个实根的和为 .
 或
或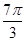
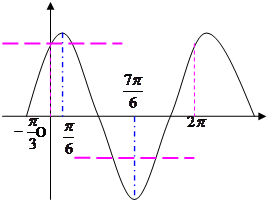
解析试题分析:因为作函数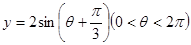 的图像,设
的图像,设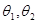 为方程的两个实根,则根据图像可知
为方程的两个实根,则根据图像可知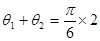 或
或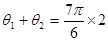 ,即
,即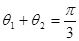 或
或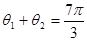 .
.
考点:新定义、函数的单调性,考查学生的分析、理解能力.

练习册系列答案
相关题目
题目内容
设 ,且方程
,且方程 有两个不同的实数根,则这两个实根的和为 .
有两个不同的实数根,则这两个实根的和为 .
 或
或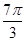
解析试题分析:因为作函数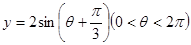 的图像,设
的图像,设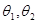 为方程的两个实根,则根据图像可知
为方程的两个实根,则根据图像可知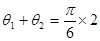 或
或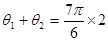 ,即
,即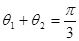 或
或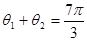 .
.
考点:新定义、函数的单调性,考查学生的分析、理解能力.
