题目内容
如图,椭圆C2
+
=1的焦点为F1,F2,|A1B1|=
,S□B1A1B2A2=2S□B1F1B2F2.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设n为过原点的直线,l是与n垂直相交与点P,与椭圆相交于A,B两点的直线|
|=1,是否存在上述直线l使
•
=0成立?若存在,求出直线l的方程;并说出;若不存在,请说明理由.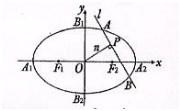
| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设n为过原点的直线,l是与n垂直相交与点P,与椭圆相交于A,B两点的直线|
| op |
| OA |
| OB |

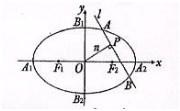
(Ⅰ)由题意可知a2+b2=7,
∵S□B1A1B2A2=2S□B1F1B2F2,
∴a=2c.
解得a2=4,b2=3,c2=1.
∴椭圆C的方程为
| x2 |
| 4 |
| y3 |
| 3 |
(Ⅱ)设A、B两点的坐标分别为A(x1,y1),B(x2,y2),假设使
| OA |
| OB |
(i)当l不垂直于x轴时,设l的方程为y=kx+m,由l与n垂直相交于P点,且|
| OP |
| |m| | ||
|
| OA |
| OB |
| -8km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
0=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=x1x2+k2x1x2+km(x1+x2)+m2
把①②代入上式并化简得(1+k2)(4m2-12)-8k2m2+m2(3+4k2)=0,③
将m2=1+k2代入③并化简得-5(k2+1)=0矛盾.即此时直线l不存在.
(ii)当l垂直于x轴时,满足|
| OP |
由A、B两点的坐标为(1,
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
当x=1时,
| OA |
| OB |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
当x=-1时,
| OA |
| OB |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
∴此时直线l也不存在.
综上所述,使
| OA |
| OB |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
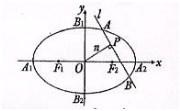 如图,椭圆C2
如图,椭圆C2 如图,椭圆Ⅰ与Ⅱ有公共的左顶点和公共的左焦点F,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心,设椭圆Ⅰ与Ⅱ的离心率分别为e1和e2,则( )
如图,椭圆Ⅰ与Ⅱ有公共的左顶点和公共的左焦点F,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心,设椭圆Ⅰ与Ⅱ的离心率分别为e1和e2,则( ) 如图,椭圆被其内接三角形分为4块,现有4种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有多少种( )
如图,椭圆被其内接三角形分为4块,现有4种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有多少种( )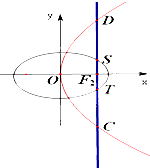 (2012•上高县模拟)如图,椭圆
(2012•上高县模拟)如图,椭圆