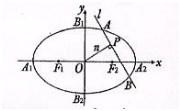
题目内容
 如图,椭圆C2
如图,椭圆C2| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设n为过原点的直线,l是与n垂直相交于点P,与椭圆相交于A,B两点的直线|
| OP |
| OA |
| OB |
分析:(Ⅰ)由题意可知a2+b2=7,a=2c,由此能够求出椭圆C的方程.
(Ⅱ)设A、B两点的坐标分别为A(x1,y1),B(x2,y2),假设使
•
=0成立的直线l存在.
(i)当l不垂直于x轴时,根据题设条件能够推出直线l不存在.
(ii)当l垂直于x轴时,满足|
|=1的直线l的方程为x=1或x=-1,由A、B两点的坐标为(1,
),(1,-
)或(-1,
),(-1,-
).当x=1时,
•
=-
≠0.当x=-1时,
•
=-
≠0.所以此时直线l也不存在.由此可知,使
•
=0成立的直线l不成立.
(Ⅱ)设A、B两点的坐标分别为A(x1,y1),B(x2,y2),假设使
| OA |
| OB |
(i)当l不垂直于x轴时,根据题设条件能够推出直线l不存在.
(ii)当l垂直于x轴时,满足|
| OP |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| OA |
| OB |
| 5 |
| 4 |
| OA |
| OB |
| 5 |
| 4 |
| OA |
| OB |
解答: 解:(Ⅰ)由题意可知a2+b2=7,
解:(Ⅰ)由题意可知a2+b2=7,
∵S□B1A1B2A2=2S□B1F1B2F2,
∴a=2c.
解得a2=4,b2=3,c2=1.
∴椭圆C的方程为
+
=1.
(Ⅱ)设A、B两点的坐标分别为A(x1,y1),B(x2,y2),假设使
•
=0成立的直线l存在.
(i)当l不垂直于x轴时,设l的方程为y=kx+m,由l与n垂直相交于P点,且|
|=1得
=1,即m2=k2+1,由
•
=0得x1x2+y1y2=0,将y=kx+m代入椭圆得(3+4k2)x2+8kmx+(4m2-12)=0,x1+x2=
,①,x1x2=
,②
0=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=x1x2+k2x1x2+km(x1+x2)+m2
把①②代入上式并化简得(1+k2)(4m2-12)-8k2m2+m2(3+4k2)=0,③
将m2=1+k2代入③并化简得-5(k2+1)=0矛盾.即此时直线l不存在.
(ii)当l垂直于x轴时,满足|
|=1的直线l的方程为x=1或x=-1,
由A、B两点的坐标为(1,
),(1,-
)或(-1,
),(-1,-
).
当x=1时,
•
=(1,
)• (1,-
)=-
≠0.
当x=-1时,
•
=(-1,
)• (-1,-
)=-
≠0.
∴此时直线l也不存在.
综上所述,使
•
=0成立的直线l不成立.
 解:(Ⅰ)由题意可知a2+b2=7,
解:(Ⅰ)由题意可知a2+b2=7,∵S□B1A1B2A2=2S□B1F1B2F2,
∴a=2c.
解得a2=4,b2=3,c2=1.
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设A、B两点的坐标分别为A(x1,y1),B(x2,y2),假设使
| OA |
| OB |
(i)当l不垂直于x轴时,设l的方程为y=kx+m,由l与n垂直相交于P点,且|
| OP |
| |m| | ||
|
| OA |
| OB |
| -8km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
0=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=x1x2+k2x1x2+km(x1+x2)+m2
把①②代入上式并化简得(1+k2)(4m2-12)-8k2m2+m2(3+4k2)=0,③
将m2=1+k2代入③并化简得-5(k2+1)=0矛盾.即此时直线l不存在.
(ii)当l垂直于x轴时,满足|
| OP |
由A、B两点的坐标为(1,
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
当x=1时,
| OA |
| OB |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
当x=-1时,
| OA |
| OB |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
∴此时直线l也不存在.
综上所述,使
| OA |
| OB |
点评:本题综合考查直线和椭圆的位置关系,解题时要认真审题,灵活地运用公式.

练习册系列答案
相关题目
 如图,椭圆Ⅰ与Ⅱ有公共的左顶点和公共的左焦点F,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心,设椭圆Ⅰ与Ⅱ的离心率分别为e1和e2,则( )
如图,椭圆Ⅰ与Ⅱ有公共的左顶点和公共的左焦点F,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心,设椭圆Ⅰ与Ⅱ的离心率分别为e1和e2,则( ) 如图,椭圆被其内接三角形分为4块,现有4种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有多少种( )
如图,椭圆被其内接三角形分为4块,现有4种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有多少种( ) (2012•上高县模拟)如图,椭圆
(2012•上高县模拟)如图,椭圆