题目内容
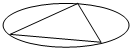
 如图,椭圆被其内接三角形分为4块,现有4种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有多少种( )
如图,椭圆被其内接三角形分为4块,现有4种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有多少种( )分析:由题意相邻两块的颜色不同,通过对涂色区域编号,分别选出2种颜色、3种颜色、4种颜色涂色,求出各自的涂色方案种数,即可得到结果.
解答:解:对涂色区域编号,如图:
分别用2色、就是1一色,2、3、4同色,涂色方法为:C42A22=12;
涂3色时,2、3同色,2、4同色,3、4同色,涂色方法是3C43A33=72;
涂4色时涂色方法是A44=24,
所以涂色方案有:12+72+24=108.
故选B.
分别用2色、就是1一色,2、3、4同色,涂色方法为:C42A22=12;
涂3色时,2、3同色,2、4同色,3、4同色,涂色方法是3C43A33=72;
涂4色时涂色方法是A44=24,
所以涂色方案有:12+72+24=108.
故选B.

点评:本题是中档题,考查排列组合计数原理的应用,考查分类讨论思想的应用,考查计算能力.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 一种颜色,且相邻两块的颜色不同,则不同的涂色方法有多少种( ) A. 124
B. 108 C.48
D. 24
一种颜色,且相邻两块的颜色不同,则不同的涂色方法有多少种( ) A. 124
B. 108 C.48
D. 24 如图,椭圆被其内接三角形分为4块,现有4种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有多少种
如图,椭圆被其内接三角形分为4块,现有4种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有多少种