题目内容
【题目】在平面直角坐标系中![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为:
的参数方程为: (
(![]() 为参数),
为参数),![]() ,
,![]() 为直线
为直线![]() 上距离为
上距离为![]() 的两动点,点
的两动点,点![]() 为曲线
为曲线![]() 上的动点且不在直线
上的动点且不在直线![]() 上.
上.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程.
的直角坐标方程.
(2)求![]() 面积的最大值.
面积的最大值.
【答案】(1)直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,曲线
,曲线![]() 的普通方程为
的普通方程为![]() (2)
(2)![]()
【解析】
(1)直线![]() 的极坐标方程
的极坐标方程![]() 利用两角差的余弦公式展开,再利用公式
利用两角差的余弦公式展开,再利用公式![]() ,将方程化成普通方程形式;对曲线
,将方程化成普通方程形式;对曲线![]() 的参数
的参数![]() 进行消参,从而得到普通方程;
进行消参,从而得到普通方程;
(2)设点![]()
![]() ,将点到直线的距离转化为三角函数的值域问题.
,将点到直线的距离转化为三角函数的值域问题.
(1)直线![]() 的极坐标方程
的极坐标方程![]() 化成
化成![]() ,
,
![]()
![]() ,
,![]() 直线
直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
曲线![]() 的参数方程化成:
的参数方程化成: .
.
平方相加得![]() ,即
,即![]()
(2)设点![]()
![]() ,则
,则![]() 到直线
到直线![]() 的距离为:
的距离为:
![]()
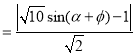 ,
,
当![]() 时,
时,![]() ,
,
设![]() 的面积为
的面积为![]() ,则
,则![]()
![]() .
.

练习册系列答案
相关题目
【题目】某企业生产A产品的质量以其质量指标值衡量,质量指标值划分等级及产品售价如下表:
质量指标值m |
|
|
|
产品等级 | 等品 | 二等品 | 三等品 |
售价(每件) | 160元 | 140元 | 120元 |
从该企业生产的A产品中抽取100件作为样本,检测其质量指标值,得到下图的频率分布直方图.
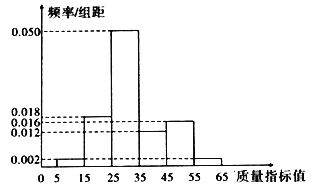
(1)根据频率分布直方图,求A产品质量指标值的中位数;
(2)用样本频率估计总体概率.现有一名顾客随机购买两件A产品,设其支付的费用为X元,求X的分布列及数学期望.