题目内容
(本小题满分16分)
高 已知数列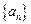 的前
的前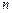 项和为
项和为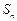 ,且满足
,且满足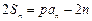 ,
,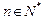 ,其中常数
,其中常数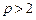 .
.
(1)证明:数列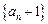 为等比数列;
为等比数列;
(2)若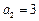 ,求数列
,求数列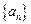 的通项公式;
的通项公式;
(3)对于(2)中数列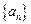 ,若数列
,若数列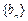 满足
满足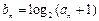 (
(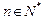 ),在
),在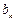 与
与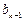 之间插入
之间插入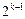 (
(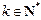 )个2,得到一个新的数列
)个2,得到一个新的数列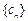 ,试问:是否存在正整数m,使得数列
,试问:是否存在正整数m,使得数列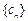 的前m项的和
的前m项的和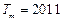 ?如果存在,求出m的值;如果不存在,说明理由.
?如果存在,求出m的值;如果不存在,说明理由.
高 已知数列
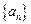 的前
的前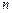 项和为
项和为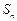 ,且满足
,且满足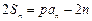 ,
,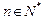 ,其中常数
,其中常数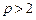 .
.(1)证明:数列
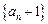 为等比数列;
为等比数列;(2)若
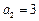 ,求数列
,求数列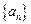 的通项公式;
的通项公式;(3)对于(2)中数列
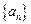 ,若数列
,若数列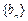 满足
满足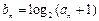 (
(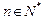 ),在
),在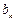 与
与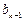 之间插入
之间插入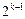 (
(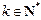 )个2,得到一个新的数列
)个2,得到一个新的数列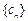 ,试问:是否存在正整数m,使得数列
,试问:是否存在正整数m,使得数列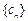 的前m项的和
的前m项的和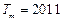 ?如果存在,求出m的值;如果不存在,说明理由.
?如果存在,求出m的值;如果不存在,说明理由.解:(1)∵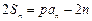 ,∴
,∴ ,∴
,∴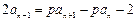 ,
,
∴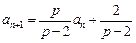 ,∴
,∴ , …………………4分
, …………………4分
∵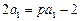 ,∴
,∴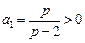 ,∴
,∴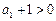
∴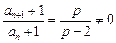 ,∴数列
,∴数列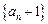 为等比数列.
为等比数列.
(2)由(1)知 ,∴
,∴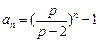 ………………8分
………………8分
又∵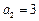 ,∴
,∴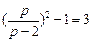 ,∴
,∴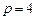 ,∴
,∴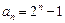 ………………10分
………………10分
(3)由(2)得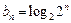 ,即
,即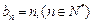 ,
,
数列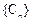 中,
中,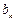 (含
(含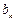 项)前的所有项
项)前的所有项 的和是:
的和是:
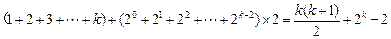 …………12分
…………12分
当k="10" 时,其和是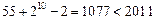
当k="11" 时,其和是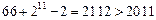
又因为2011-1077=934=467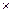 2,是2的倍数 …………………………14分
2,是2的倍数 …………………………14分
所以当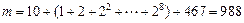 时,
时,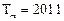 ,
,
所以存在m=988使得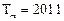 ……………………………16分
……………………………16分
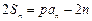 ,∴
,∴ ,∴
,∴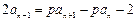 ,
,∴
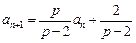 ,∴
,∴ , …………………4分
, …………………4分∵
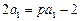 ,∴
,∴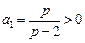 ,∴
,∴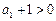
∴
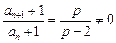 ,∴数列
,∴数列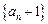 为等比数列.
为等比数列. (2)由(1)知
 ,∴
,∴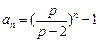 ………………8分
………………8分又∵
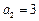 ,∴
,∴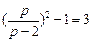 ,∴
,∴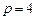 ,∴
,∴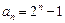 ………………10分
………………10分(3)由(2)得
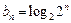 ,即
,即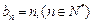 ,
,数列
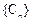 中,
中,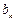 (含
(含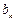 项)前的所有项
项)前的所有项 的和是:
的和是: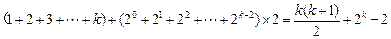 …………12分
…………12分当k="10" 时,其和是
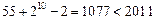
当k="11" 时,其和是
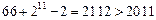
又因为2011-1077=934=467
 2,是2的倍数 …………………………14分
2,是2的倍数 …………………………14分所以当
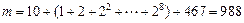 时,
时,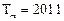 ,
,所以存在m=988使得
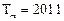 ……………………………16分
……………………………16分略

练习册系列答案
相关题目
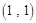 ,
,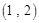 ,
,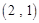 ,
,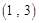 ,
,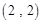 ,
,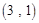 ,
,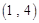 ,
,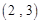 ,
,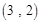 ,
,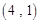 ,……,则第
,……,则第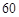 个数对是
个数对是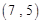
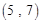
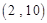
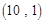
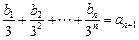 成立,求数列{bn}的通项
成立,求数列{bn}的通项 公式.
公式. 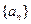 的前
的前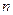 项和为
项和为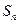 ,对一切
,对一切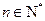 ,点
,点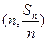 都在函数
都在函数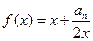 的图象上.
的图象上.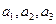 及数列
及数列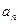 ;
;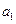 ),(
),(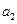 ,
,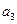 ),(
),(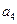 ,
,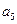 ,
,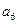 ),(
),(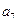 ,
,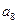 ,
,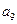 ,
,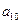 );(
);(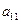 ),(
),(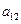 ,
,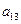 ),(
),(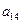 ,
,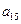 ,
,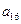 ),(
),(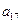 ,
,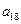 ,
,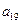 ,
,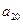 );(
);(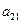 ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为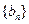 ,求
,求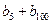 的值;
的值;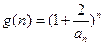 (
(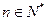 ),求证:
),求证: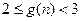 .
.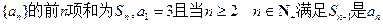 与-3的等差中项。
与-3的等差中项。 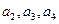 ;
;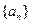 的通项公式.
的通项公式.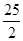 ,偶数项的和为15,则这个数列的第六项是()
,偶数项的和为15,则这个数列的第六项是()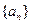 为等差数列,
为等差数列,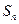 为数列
为数列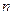 项和,已知
项和,已知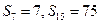 ,
,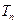 为数列
为数列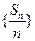 的前
的前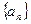 中,首项
中,首项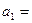
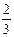 ,
,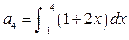 ,则公比
,则公比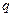 为 .
为 .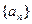 中,
中,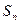 是其前
是其前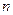 项和,
项和,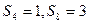 ,则
,则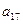 +
+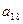 +
+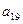 +
+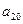 =
= 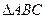 中,角
中,角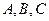 的对边分别为
的对边分别为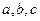 ,且
,且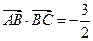 ,
,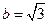 ,求
,求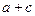 的值;
的值;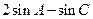 的取值范围。
的取值范围。