题目内容
2. 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:(Ⅰ) 估计这500件产品质量指标值的样本平均数$\overline x$.
(Ⅱ)由频率分布直方图可以认为,这种总产品的质量指标值Z近似服从正态分布N(μ,δ2),其中μ近似为样本平均数$\overline x$,δ2近似为样本方差s2.(由样本估计得样本方差为s2=150)
(i)利用该正态分布,求P(Z<212.2);
(ii)若将这种产品质量指标值位于这三个区间(-∞,187.8)(187.8,212.2)(212.2.,+∞)的等级分别为二等品,一等品,优质品,这三类等级的产品在市场上每件产品的利润分别为2元,5元,10元.某商户随机从该企业批发100件这种产品后卖出获利,记X表示这100件产品的利润,利用正态分布原理和(i)的结果,求EX.
附:$\sqrt{150}$≈12.2.若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,P(μ-2δ<Z<μ+2δ)=0.9544.
分析 (1)运用离散型随机变量的期望和方差公式,即可求出;
(2)(i)由(1)知Z~N(200,150),从而求出P(187.8<Z<212.2),P(200<Z<212.2)=0.3413,即可得出结论;
(ii)设这种产品每件利润为随机变量Y,求出E(Y),即可求得EX.
解答 解:(1)取个区间中点值为区间代表计算得:
$\overline{x}$=170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
s2=(-30)2×0.02+(-20)2×0.09+(-10)2×0.22+0×0.33+102×0.24+202×0.08+302×0.02=150.
(2)(i)由(1)知Z~N(200,150),从而P(187.8<Z<212.2)=P(200-12.2<Z<200+12.2)=0.6826,
所以P(200<Z<212.2)=0.3413,
所以P(Z<212.2)=0.8413
(ii)设这种产品每件利润为随机变量Y,其分布列为
| Y | 2 | 5 | 10 |
| P | 0.1587 | 0.6826 | 0.1587 |
E(x)=E(100Y)=100×5.3174=531.74.
点评 本题主要考查离散型随机变量的期望和方差,以及正态分布的特点及概率求解,考查运算能力.

练习册系列答案
相关题目
12.设等差数列{an}的前n项和为Sn,且满足S20>0,S21<0,则$\frac{S_1}{a_1},\frac{S_2}{a_2},…,\frac{{{S_{21}}}}{{{a_{21}}}}$中最大的项为( )
| A. | $\frac{s_8}{a_8}$ | B. | $\frac{{{s_{10}}}}{{{a_{10}}}}$ | C. | $\frac{{{s_{11}}}}{{{a_{11}}}}$ | D. | $\frac{{S}_{9}}{{a}_{9}}$ |
7.在区间(2kπ+$\frac{π}{2}$,2kπ+π),k∈Z上存在零点的函数是( )
| A. | y=sin2x | B. | y=cos2x | C. | y=tan2x | D. | y=sin2x |
14.复数$\frac{1}{2-i}$的虚部为( )
| A. | $\frac{1}{5}i$ | B. | $\frac{1}{5}$ | C. | $\frac{\sqrt{5}}{5}i$ | D. | $\frac{\sqrt{5}}{5}$ |
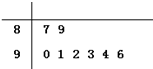 某校高二年级8个班参加合唱比赛的得分如面茎叶图所示,则这组数据的中位数和平均数为91.5和91.5.
某校高二年级8个班参加合唱比赛的得分如面茎叶图所示,则这组数据的中位数和平均数为91.5和91.5.