题目内容
|x-2|＞0的解集为R． （判断对错）
考点：绝对值不等式的解法
专题：计算题,不等式的解法及应用
分析：由绝对值的意义可得，|x-2|＞0即为
或
，分别解出它们，再求并集即可．
|
|
解答：
解：|x-2|＞0即为
或
具有x＞2或x＜2，
即解集为{x|x≠2且x∈R}．
故答案为：错．
|
|
具有x＞2或x＜2，
即解集为{x|x≠2且x∈R}．
故答案为：错．
点评：本题考查绝对值不等式的解法，考查运算能力，属于基础题．
练习册系列答案
相关题目
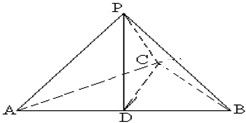如图，已知三棱锥P-ABC，D为AB的中点，且△PDB是正三角形，PA⊥PC．求证：PC⊥BC．