题目内容
9.在△ABC中,已知A、B、C成等差数列,且边AC=2,则$\overrightarrow{AB}•\overrightarrow{AC}$的最大值为( )| A. | $\frac{{4\sqrt{3}}}{3}$+2 | B. | 4 | C. | 4-$\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$+1 |
分析 根据条件可得到B=$\frac{π}{3}$,也就是B为锐角,根据数量积的计算公式即可得到$\overrightarrow{AB}•\overrightarrow{AC}=2|\overrightarrow{AB}|cosA$,结合$|\overrightarrow{AB}|cosA$的几何意义即可知道当AC⊥BC时$|\overrightarrow{AB}|cosA$取到最大值2,这样即可得出$\overrightarrow{AB}•\overrightarrow{AC}$的最大值.
解答 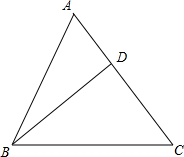 解:A、B、C成等差数列;
解:A、B、C成等差数列;
∴2B=A+C;
又A+B+C=π;
3B=π,B=$\frac{π}{3}$;
$\overrightarrow{AB}•\overrightarrow{AC}=|\overrightarrow{AB}||\overrightarrow{AC}|cosA=2|\overrightarrow{AB}|cosA$;
如图,过B作BD⊥AC,垂足为D,则:
由图可看出$|\overrightarrow{AB}|cosA=AD$;
只有当D和C点重合时,$|\overrightarrow{AB}|cosA$取到最大值AC=2;
∴$\overrightarrow{AB}•\overrightarrow{AC}$的最大值为4.
故选:B.
点评 考查等差数列的定义,向量数量积的计算公式,余弦函数的定义,以及数形结合解题的方法.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
18.观察下列的规律:$\frac{1}{1},\frac{1}{2},\frac{2}{1}$,$\frac{1}{3},\frac{2}{2},\frac{3}{1}$,$\frac{1}{4},\frac{2}{3},\frac{3}{2},\frac{4}{1}$…则第93个是( )
| A. | $\frac{1}{8}$ | B. | $\frac{2}{13}$ | C. | $\frac{8}{7}$ | D. | $\frac{1}{14}$ |
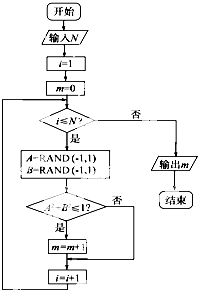 如图所示的程序框图可用来估计π的值(假设函数RAND(-1,1)是产
如图所示的程序框图可用来估计π的值(假设函数RAND(-1,1)是产