题目内容
已知等差数列
的前n项和为
，某三角形三边之比为
,则该三角形的最大角为
的前n项和为，某三角形三边之比为,则该三角形的最大角为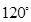 
解：令n=1，得到a1=S1=2a+1，令n=2，得到a1+a2=S2=5a+4，
所以a2=3a+3，故公差d=（3a+3）-（2a+1）=a+2，
所以Sn=n（2a+1）+n(n-1) /2 （a+2）="a+2" /2 n2+（2a+1-a+2/ 2 ）n=（a+1）n2+a，
得到a=0，所以等差数列的首项a1=1，公差d=2，
所以三角形三边之比为3：5：7，设最大的角为α，三边分别为3k，5k，7k，
所以cosα=3k2+5k2-7k2/ 2×3k×5k ="-1" 2 ，又α∈（0，180°），
则该三角形最大角α为120°．
故答案为：120°
所以a2=3a+3，故公差d=（3a+3）-（2a+1）=a+2，
所以Sn=n（2a+1）+n(n-1) /2 （a+2）="a+2" /2 n2+（2a+1-a+2/ 2 ）n=（a+1）n2+a，
得到a=0，所以等差数列的首项a1=1，公差d=2，
所以三角形三边之比为3：5：7，设最大的角为α，三边分别为3k，5k，7k，
所以cosα=3k2+5k2-7k2/ 2×3k×5k ="-1" 2 ，又α∈（0，180°），
则该三角形最大角α为120°．
故答案为：120°
练习册系列答案
阅读快车系列答案
相关题目
的两个根， 且2cos(A+B)=1.
则AD和BC所成的角是（ ）
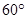
，且△ABC的面积为
，则AC的长为_____．
中，角A、B、C的对边分别为a，b，c。角A，B，C成等差数列。
的值；
的值。
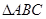中，角
、
、
的对边分别是
，
，
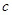，已知
．
，求
方向300
的海面P处，并以
的速度向西偏北
方向移动。台风侵袭的范围为圆形区域，当前半径为60
的速度不断增大，问几时后该城市开始受到台风的侵袭？
中，
，
，
分别为内角
，
，
所对的边，且满足
，且
，
，求
的值．