题目内容
.空间四边形ABCD中,M,N分别是AB和CD的中点,AD=BC=6,MN= 则AD和BC所成的角是( )
则AD和BC所成的角是( )
 则AD和BC所成的角是( )
则AD和BC所成的角是( )A. | B. | C.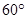 | D. |
B
解:如图所示:取BD的中点G,连接GM,GN.空间四边形ABCD中,AD=BC=2,E、F分别是AB、CD的中点,
故MG是三角形ABD的中位线,GN是三角形CBD的中位线,故∠EGF(或其补角)即为AD与BC所成的角.△MGN中,MN= ,由余弦定理可得 18=32+32-2cos∠MGN,∴cos∠MGN=0,
,由余弦定理可得 18=32+32-2cos∠MGN,∴cos∠MGN=0,
∴∠MGN=90°,故AD与BC所成的角为90°,故答案为选B.
故MG是三角形ABD的中位线,GN是三角形CBD的中位线,故∠EGF(或其补角)即为AD与BC所成的角.△MGN中,MN=
 ,由余弦定理可得 18=32+32-2cos∠MGN,∴cos∠MGN=0,
,由余弦定理可得 18=32+32-2cos∠MGN,∴cos∠MGN=0,∴∠MGN=90°,故AD与BC所成的角为90°,故答案为选B.

练习册系列答案
相关题目
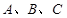 为
为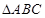 的三内角,且其对边分别为
的三内角,且其对边分别为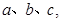 若
若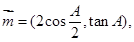
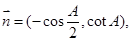 且
且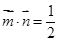 .
.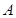 ;
;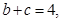
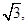 求
求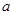 .
. ,则三角形的形状一定是 .(填写“锐角、钝角、直角”)
,则三角形的形状一定是 .(填写“锐角、钝角、直角”) 的前n项和为
的前n项和为 ,某三角形三边之比为
,某三角形三边之比为 ,则该三角形的最大角为
,则该三角形的最大角为  ,AC=4,则△ABC的面积等于
,AC=4,则△ABC的面积等于  中,已知
中,已知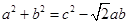 ,则
,则
 则b=______.
则b=______. 中,
中, ,则B的大小为 .
,则B的大小为 . 中,已知三边
中,已知三边 、
、 、
、 满足
满足 ,则
,则 .
.