题目内容
设x,y,z∈R,且满足:x2+y2+z2=1,x+2y+3z=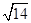 ,则x+y+z=________.
,则x+y+z=________.
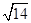 ,则x+y+z=________.
,则x+y+z=________.
由柯西不等式,得
(x2+y2+z2)(12+22+32)≥(x+2y+3z)2,
∴(x+2y+3z)2≤14,则x+2y+3z≤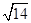 ,
,
又x+2y+3z=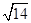 ,
,
∴x=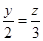 ,
,
因此x=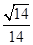 ,y=
,y= ,z=
,z=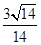 ,
,
于是x+y+z= .
.
(x2+y2+z2)(12+22+32)≥(x+2y+3z)2,
∴(x+2y+3z)2≤14,则x+2y+3z≤
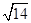 ,
,又x+2y+3z=
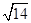 ,
,∴x=
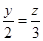 ,
,因此x=
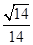 ,y=
,y= ,z=
,z=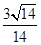 ,
,于是x+y+z=
 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
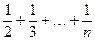 ,当n≥2,n
,当n≥2,n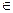 N*时,用数学归纳法证明:n+f(1)+f(2)+…+f(n-1)=nf(n)。
N*时,用数学归纳法证明:n+f(1)+f(2)+…+f(n-1)=nf(n)。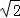 .M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
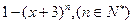 能被
能被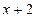 整除
整除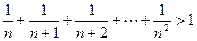 (
(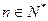 且
且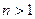 )
) ,则
,则 的最大值为______.
的最大值为______.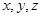 ,
,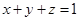 ,求证:
,求证: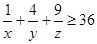 ;
;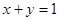 ,求
,求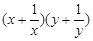 的最小值。
的最小值。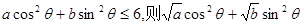 的最大值为 .
的最大值为 .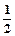 x2-1恒成立,求实数a的取值范围。
x2-1恒成立,求实数a的取值范围。