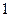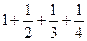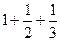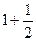题目内容
（12分）设f(n)=1+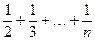
，当n≥2，n
N*时，用数学归纳法证明：n+f(1)+f(2)+…+f(n－1)=nf(n)。
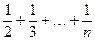，当n≥2，nN*时，用数学归纳法证明：n+f(1)+f(2)+…+f(n－1)=nf(n)。见解析
（1）n=2时，左=2+f(1)=3=2(1+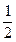
)=2f(2)=右，成立。
（2）假设n=k时，有k+f(1)+f(2)+…+f(k－1)=kf(k)，
则当n=k+1时，左=k+1+f(1)+f(2)+…+f(k－1)+f(k)，
右=(k+1)f(k+1)
左=1+f(k)+k+f(1)+f(2)+…+f(k－1)=1+f(k)+kf(k)=(k+1)[f(k)+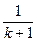
]=(k+1)f(k+1)=右
∴n=k+1时，等式成立
由（1）、（2）可知对n≥2，n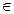
N*等式都成立
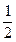)=2f(2)=右，成立。（2）假设n=k时，有k+f(1)+f(2)+…+f(k－1)=kf(k)，
则当n=k+1时，左=k+1+f(1)+f(2)+…+f(k－1)+f(k)，
右=(k+1)f(k+1)
左=1+f(k)+k+f(1)+f(2)+…+f(k－1)=1+f(k)+kf(k)=(k+1)[f(k)+
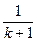]=(k+1)f(k+1)=右∴n=k+1时，等式成立
由（1）、（2）可知对n≥2，n
N*等式都成立
练习册系列答案
相关题目
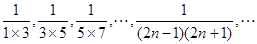，计算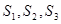
，根据计算结果，猜想
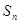的表达式，并用数学归纳法给出证明.
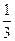，记为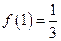
；
当从A口输入自然数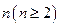
时，在B口得到的结果
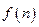是前一个结果
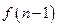的
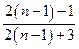倍；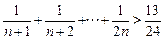
.
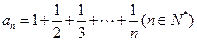，是否存在整式
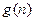，使得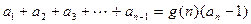
对n≥2的一切自然数都成立?并试用数学
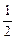成等比数列.
N*,1-
+
-
+…+
-
=
+
+…+
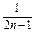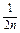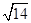，则x＋y＋z＝________.
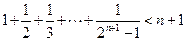”验证n=1成立时,左边所得项是（ ） 
