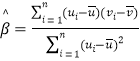题目内容
【题目】甲、乙两名同学参加一项射击游戏，两人约定，其中任何一人每射击一次，击中目标得2分，未击中目标得0分.若甲、乙两名同学射击的命中率分别为
和p，且甲、乙两人各射击一次所得分数之和为2的概率为
，假设甲、乙两人射击互不影响.
（1）求p的值；
（2）记甲、乙两人各射击一次所得分数之和为X，求X的分布列和均值
.
【答案】（1）
；（2）分布列见解析；均值为
.
【解析】
（1）利用相互独立事件的概率乘法公式即可求解.
（2）由已知X的取值分别为0，2，4，利用相互独立事件的概率乘法公式即可求出分布列，再利用均值的公式即可求解.
解：（1）设“甲射击一次，击中目标”为事件A，“乙射击一次，击中目标”为事件B，
“甲射击一次，未击中目标”为事件
，“乙射击一次，未击中目标”为事件
，.
则
，
，
，
.
依题意得
，.
解得
，故p的值为.
（2）由已知X的取值分别为0，2，4，且
，
.
，.
，.
，.
∴X的分布列为
X | 0 | 2 | 4 |
P |
|
|
|
∴
.
练习册系列答案
优等生题库系列答案
相关题目
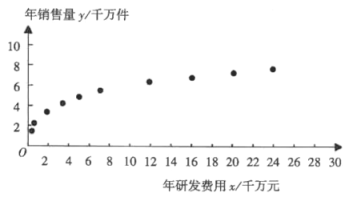
【题目】某校2011年到2019年参加“北约”“华约”考试而获得加分的学生人数（每位学生只能参加“北约”“华约”中的一种考试）可以通过以下表格反映出来，（为了方便计算，将2011年编号为1，2012年编号为2，依此类推）
年份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数y | 2 | 3 | 5 | 4 | 5 | 7 | 8 | 10 | 10 |
（1）求这九年来，该校参加“北约”“华约”考试而获得加分的学生人数的平均数和方差；
（2）根据最近五年的数据，利用最小二乘法求出y与x的线性回归方程，并依此预测该校2020年参加“北约”“华约”考试而获得加分的学生人数．（最终结果精确至个位）
参考数据：回归直线的方程是
，其中
，
，
，
．
